In a lecture titled "Where are the real numbers?" before the Nationale Wiskunde Dagen 2008 I adressed the problem of proving that the set of rational numbers is strictly smaller than the set of real numbers. Surely there are many proofs, such as showing that square root of 2 is irrational or use the fact that rational numbers have periodic decimal expansions. A third one, which I particularly liked, is accompanied by pictures. In particular, playing with these pictures raises a number of questions which goes down quite deeply into the theory of diophantine approximation.

Here is the idea. Consider the real line between 0 and 1. We now cover up the rational number p/q with a colored disk centered at p/q. We do this for all rational numbers and hope that after doing this a number of points will be left uncovered, thus proving that there are more real numbers than rational numbers. Of course this is a naive approach which is certainly doomed to failure if we take all disks equally big. Therefore we let the radius of the disks depend on the value of the denominator q.

We now let you do the following increasingly difficult problems.

• Exercise 1 (easy) Suppose we take disks of radius 1/q. Show that with this choice eventually all real numbers strictly between 0 and 1 will be covered by a disk.
• Exercise 2 (a bit harder) Suppose we take disks of radius c/q, where c is a positive number. Show that with this choice eventually all real numbers strictly between 0 and 1 will be covered by a disk.
• Exercise 3 (equally hard) Suppose we take disks of radius 1/q^2. Show that with this choice eventually all real numbers strictly between 0 and 1 will be covered by a disk.
• Exercise 4 (very hard if you do not know continued fractions) Suppose we take disks of radius 0.4/q^2. Show that with this choice eventually all but one real numbers strictly between 0 and 1 will be covered by a disk. The one exception is 1 divided by the golden ratio.
• Exercise 5 (not so hard) Suppose we take disks of radius c/2^(p+q+1). Show that the total space occupied by the disks is at most c. Therefore, by taking c=1/1000 for example, we see that a very small fraction of the real numbers is rational. All the rest is irrational.

It is very nice to visualise the proces of covering the real line with the disks.
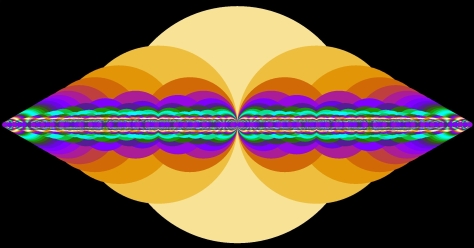
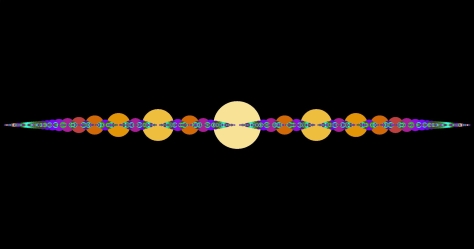
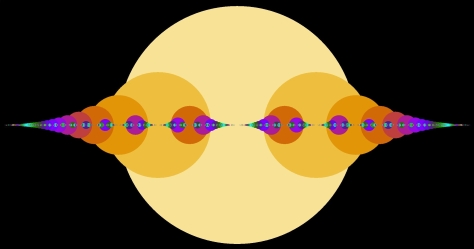
Here are the disk sizes 0.5/q and 0.1/q:

And here the disk sizes 1/q^2 and 0.2/q^2:

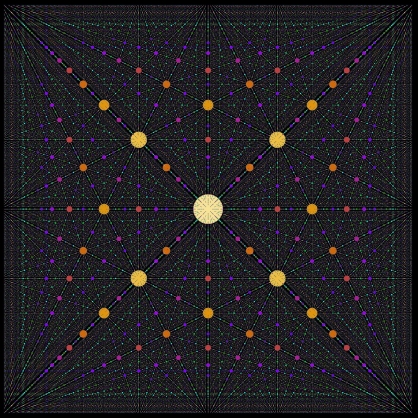
Out of curiosity I asked myself the following question. Suppose we cover every rational point (p/q,r/q) in the unit square by a disk. What would the result then be? For reasons from diophantine approximation it turns out that disk radius of the form c/q^1.5 is the best choice. The results for 0.3/q^1.5 and 0.1/q^1.5 are displayed at the top of this page.

Of course you may want to experiment yourself with different disk sizes and see what happens. To that end you should have a postscript viewer installed on your computer (ghostview is a good choice) and download the following two postscript files:

• realdisks.ps (Disks on the unit interval)
• realdisks2D.ps (Disks on the unit square)

Then load either one of the files in the postscript viewer and look at the result. If you want to change parameters, simply load one of these files in a plain text editor (like Notepad, NOT MSWord), change some of the values, save and view again in the postscript viewer.