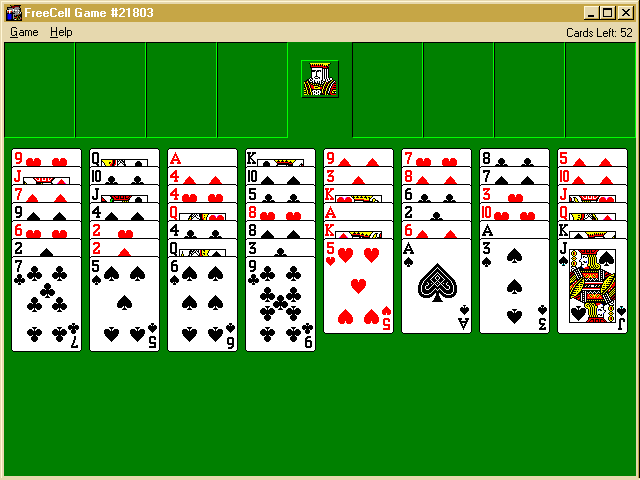
One of the additional programs, that are included with Windows'95, Microsofts operating system for personal computers, is a (computer program that simulates a) card puzzle game, called FreeCell. In this card game, the player is given an arrangement of all 52 cards of a standard deck of cards in eight columns, i.e., four columns with seven cards, and four columns with six cards. The cards are shown open face, i.e., the player knows the exact location of all cards. Additionally, there are four free cells, and four home cells. The object of the game is to move all cards to the home cells, moving cards one at the time, under the following rules:
As an example, look at the opening setup in Figure 1.

Possible moves in the starting position shown above are e.g., moving the Ace of Spades to a home cell, or moving the five of Hearts below the Six of Spades. When we would move the Seven of Clubs to a free cell, we can then move the 2 of Spades and the 3 of Spades to the home cell with the Spades. (Note: this position 21803 is solvable.)
Object of the game is to move such that finally all cards are on the home cells.
In the Help-file of the program, the following statement is made:
It is believed (although not proven) that every game is winnable.
This note disproves this conjecture, by showing a starting position for Free Cell that cannot be won.
Actually, recently, it was verified by a computer search that even one instance generated by the Freecell program is not winnable [ The Internet FreeCell Project, link no longer functional].