Planaire grafen

Planaire grafen zijn grafen die zo getekend kunnen worden in R2 dat kanten elkaar niet snijden (we laten de formele definitie weg). Een platte graaf is een planaire graaf gegeven samen met een planaire inbedding (Engels: plane graph).

Bij een planaire inbedding van een platte graaf kan men vlakken onderscheiden: gedeelten van R2 die maximaal en samenhangend zijn en geen punten op lijnen bevatten. Vlakken (faces) identificeren we ook door de knopen die het vlak afschermen.

Voorbeeld:

Vlakken:

Het buitenvlak (exterior face) is een bijzonder vlak: het is het enige vlak met een oneindig groot oppervlak.

Als G=(V,E) planair is, en v in V dan bestaat er een inbedding die v op het buitenste vlak afbeeldt.

Een sterker lemma is het volgende:

Lemma.
Als G=(V,E) planair is, en F is een vlak in een inbedding van G, dan bestaat er een inbedding die F als buitenste vlak heeft.

Het gevolg is dat de graaf binnenstebuiten wordt gekeerd: F wordt dan het buitenvlak.

Lemma.
Een graaf G=(V,E) is planair, dan en slechts dan als iedere dubbelsamenhangende component van G planair is. Een dubbelsamenhangende component van G is een maximale verzameling kanten zodat elk paar kanten in de verzameling op een gemeenschappelijke simpele cycle ligt.

Bewijs
(=> )

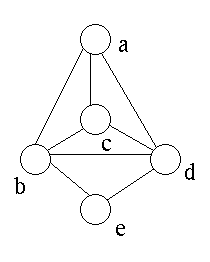
Triviaal. Als G planair is, moeten al zijn componenten natuurlijk ook planair zijn.

(<= )

Als G niet samenhangend is: beschouw iedere component afzonderlijk.

Stel G is samenhangend. We gebruiken nu inductie naar het aantal dubbelsamenhangende componenten. is er één zo’n component, dan zijn we klaar.

Anders is er een dubbelsamenhangende component die slechts één knoop gemeen heeft met de rest van G. (Waarom? Bewijs dit zelf.) Noem deze knoop v. Teken de graaf die we krijgen door deze dubbelsamenhangende component (met uitzondering van v) uit G weg te halen (inductie). Teken de dubbelsamenhangende component, zodat v op het buitenvlak ligt. Door deze laatste tekening genoeg te verkleinen en eventueel wat te vervormen, kunnen we ‘m invoegen bij v in de andere tekening en krijgen we een planaire inbedding van G.



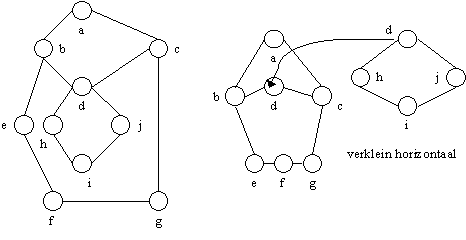
Het doel is een algoritme te krijgen dat test of een graaf planair is. Het vorige lemma helpt hierbij al een beetje: we kunnen de graaf eerst splitsen in zijn dubbelsamenhangende componenten en deze afzonderlijk te bekijken.

Stelling (Euler).
Als G=(V,E) planair is, dan geldt: |E| <= 3|V| - 6

We zien dat we mogen aannemen dat |E| = O(|V|): begin met het tellen van het aantal kanten, en als dat groter is dan 3|V| - 6 stoppen we en is de graaf niet planair.

Als we een platte graaf hebben kunnen we de duale graaf maken. Neem een knoop in de duale graaf voor elk vlak en laat twee knopen in de duale graaf grenzen als de vlakken in de originele graaf grenzen.

Bekend is de stelling van Kuratowski:

Definitie
G en H zijn homeomorph, als ze beide uit dezelfde graaf verkregen kunnen worden door nieuwe knopen van graad 2 op de kanten in te voegen.



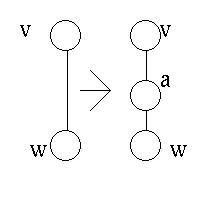
Stelling (Kuratowski)
G is planair <=> G bevat geen deelgraaf die homeomorf is met K₅ of K_3,3.



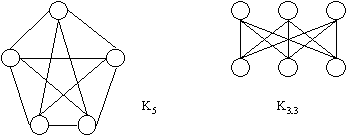
Een variant is de stelling van Wagner:

Stelling (Wagner)


G is planair <=> G bevat niet K₅ of K_3,3 als minor.

Deze stellingen helpen echter niet veel om te testen of een graaf planair is. We zullen hier het algoritme van Booth en Lueker bekijken.

De basisideeën hierbij zijn:

1. We maken een zogenaamde s-t nummering van G
2. knopen worden één voor één toegevoegd
3. een PQ-boom wordt als datastructuur gebruikt om de graaf in op te slaan

Definitie
Stel G=(V,E) is biconnected, s, t in V. Een s-t nummering van de dubbelsamenhangende graaf G=(V,E) is een bijectieve functie g : V -> {1, 2, ..., |V|} met

• s, t in V
• g(s) = 1
• g(t) = |V|
• Voor elke knoop v in V - {s, t}: v grenst aan knopen u en w met g(u) < g(v) < g(w)

We zullen nu zien dat een s-t nummering bestaat voor elke kant (s, t) in E, en in lineaire (O(V+E)) tijd gevonden kan worden.

Begin met een depth-first search op G, startend in t, en als eerste gaan we over een kant (t, s). Dus: d[t] = 1 en d[s] = 2. Herinner dat d[x] de discovery time was van knoop x.

Definieer (als in Introduction to Algorithms blz. 496):

low[v] =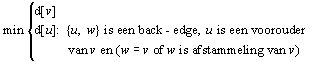

We bedoelen hierbij voorouder en afstammeling in de DFS boom.

Met DFS berekenen we alle d- en f-waarden, en voor alle kanten of ze tree-edge of back-edge zijn. We berekenen ook alle low[v] waarden voor alle v.

We definiëren eerst de "padvind" procedure.

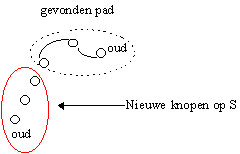
Knopen en kanten worden gemarkeerd met "oud" en "nieuw". Initieel zijn alle knopen en kanten nieuw, behalve s, t en (s, t) die oud zijn. De padvind procedure wordt aangeroepen met een knoop v in V als parameter en vindt een pad naar of vanuit v.

Padvind(v : knoop)

if er is een nieuwe backedge (v, w) met d[w] < d[v] (w is een voorouder van v)

then markeer (v, w) oud

Rapporteer het pad (v, w)

elseif er is een nieuwe tree-edge (v, w) met d[w] > d[v] (w is een kind van v)

then Rapporteer als pad:

• eerst kant (v, w),
• dan het pad wat low[w] definieert: d.w.z.: ga omlaag en neem dan 1 back-edge naar knoop u met d[u] = low[w]



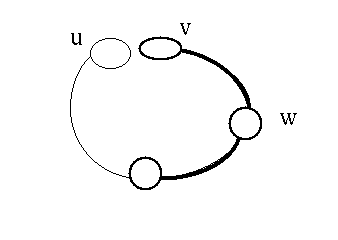
elseif er is een nieuwe back-edge (w, v) met d[w] > d[v] (w is afstammeling)



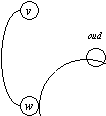
then Rapporteer als pad:

• ga over kant (v, w) naar w
• ga vanuit w omhoog in de boom over tree-

edges totdat je een oude knoop tegenkomt.

Markeer alle knopen en kanten op dit pad als oud

else (v grenst alleen aan oude kanten) Rapporteer een leeg pad

endif

Wanneer we de padvindprocedure alleen aanroepen vanuit oude knopen v =/ t dan zijn steeds alle voorouders van een oude knoop ook oud.

Bewijs
Dit is een invariant van de procedure. Initieel is dit natuurlijk waar:



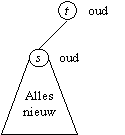
Het is makkelijk in te zien dat de invariant behouden blijft.

Gevolg
Als G dubbelsamenhangend is, en de padvindprocedure alleen met oude knopen v =/ t wordt aangeroepen, dan:

• produceert elke aanroep vanuit v een pad van v door nieuwe knopen en kanten naar een andere oude knoop
• als alle kanten die aan v grenzen oud zijn, dan produceert het algoritme een leeg pad

Bewijs
Alleen het tweede geval van de procedure behoeft nog bewijs. Dit kan gezien worden met behulp van de eigenschappen van het algoritme dat de dubbelsamenhangende componenten bepaalt.

Als namelijk low[w] >= d[v] dan is v een separatieknoop: wanneer we v weghalen is w niet meer verbonden met de ouder van v in T (deze bestaat, want v /= t). Nu is low[w] < d[v] dus low [w] is een voorouder van v en die is door de aanname oud.

Het algoritme gebruikt een stack S die initieel leeg is.

Algoritme

i := 1;

Push(t);

Push(s);

repeat

laat v het bovenste element zijn van S

Pop(v)

if v =/ t

then Padvind(v);

if gerapporteerd pad is leeg

then g(v) := i; i := i + 1

else stel gerapporteerde pad is (v, u₁, …, u_l, w). Zet u_l, u_l-1, …, u₂, u₁, v op S
(in deze volgorde, dus v komt bovenop)

endif

endif

until v = t

g(t) := I

Stelling
Dit algoritme berekent een s-t nummering van een dubbelsamenhangende graaf.

Bewijs
Merk de volgende invarianten en eigenschappen van het algoritme op:

• Geen enkele knoop komt ooit twee of meer keer voor op S
• Alle knopen op S zijn oud
• Een knoop wordt alleen dan permanent uit S verwijderd als al zijn aangrenzende kanten oud zijn
• Wanneer v op S staat, zal niets dat onder v op S staat een nummer krijgen totdat v een nummer krijgt

Claim

Iedere knoop komt eens op S voordat t van S verwijderd wordt, en er komen geen knopen onder t op S.

Bewijs van de claim
Kijk naar v =/ s, t. Er bestaat een simpel pad van v naar s dat niet door t gaat (omdat G dubbelsamenhangend is). Stel dat dit pad s = u₁, …, u_l = v is. Met inductie naar m bewijzen we: u_m komt eens op S.

• m = 1 is triviaal
• Stel u_m-1 komt eens op S. Voordat t verwijderd wordt, wordt u_m-1 verwijderd van S, en dat gebeurt pas als alle grenzende kanten oud zijn, dus ook de kant (u_m-1, u_m). Maar nadat die kant oud is, zal u_m ook zeker op S staan of gestaan hebben

Dus: iedere knoop wordt eens van S verwijderd, en krijgt dan ook een nummer. Dus g is een bijectieve functie V -> {1, ... , |V|}.

Natuurlijk geldt g(s) = 1, want s begint bovenop S. Natuurlijk is ook g(t) = |V|, want iedere keer als een knoop genummerd wordt, wordt i met 1 verhoogd. Iedere andere knoop v wordt op S gezet als deel van een pad (als interne knoop van zo’n pad).



Dus: er zit een aangrenzende knoop onder en een aangrenzende knoop boven v op de stack. De een krijgt een nummer wat 1 hoger is dan het nummer van v en de andere een nummer wat 1 lager is. QED

Het algoritme gebruikt (V+E) = O(E) tijd, DFS kost namelijk O(V+E), en bij het padvinden wordt iedere kant in totaal één keer gebruikt. Het aantal push operaties op de stack is precies |E| + 1. O(V+E) = O(E) tijd, G is namelijk samenhangend.

Zie nu blz. 372 van het artikel van Booth en Lueker.

Neem nu aan dat G=(V,E) een dubbelsamenhangende graaf is met een s-t nummering. We schrijven V = {1, 2, …, n} waarbij het nummer van de knoop z’n nummer is in de s-t nummering (dus bijvoorbeeld s = 1 en t = n). We richten nu elke kant: elke kant wordt van de knoop met het lagere nummer naar de knoop met het hogere nummer gericht. Op deze manier wordt G een gerichte acyclische graaf.

Knoop 1 (s) is de bron van G, en heeft ingraad 0. Knoop n (t) is de put van G, en heeft uitgraad 0. Omdat we een s-t nummering hebben zijn er verder geen bronnen of putten in G. We definiëren het volgende: V_k = {1, 2, …, k} en G_k = [V_k]

Stel G is planair en stel dat we een planaire inbedding van G hebben. Voor elke k ≤= n: als we de inbedding beperken tot G_k dan liggen alle knopen in V-V_k in hetzelfde vlak van deze inbedding.



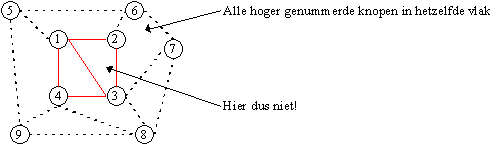
Bewijs
Stel vlak F bevat hoger genummerde knopen (d.w.z. knopen in V-V_k) De hoogst genummerde knoop in F moet een put zijn. Maar G heeft maar één put, dus is er ook maar één zo’n vlak.

Idee van het algoritme (het gaat hier om de grote lijn, niet om de details)

• Maak een s-t nummering
• Beschouw G₁
• Voeg één voor één knopen toe: we houden een PQ-boom bij die als bladeren de uitgaande kanten uit de huidige graaf G_k heeft

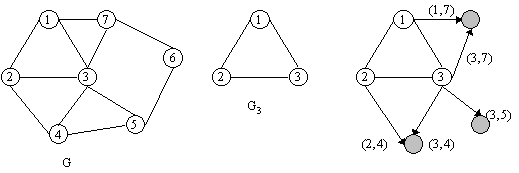
Van graaf G_k maken we een graaf B_k: voor elke kant van een knoop in V_k naar een knoop in V-V_k nemen we een kant vanuit hetzelfde beginpunt naar een nieuwe knoop.

Voorbeeld 1



Voorbeeld 2



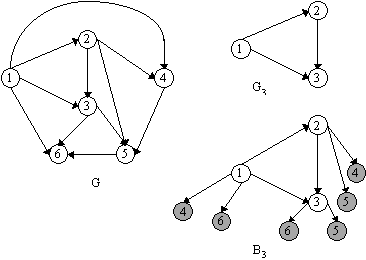
Er bestaat een planaire inbedding van B_k zodat alle extra kanten op het buitenvlak liggen, als G planair is (Lemma 2). Een van de extra kanten zal altijd (zolang k ≤ n = |V|) de kant (1, n) zijn.

We berekenen B_k als volgt:

• Knoop 1 zit op het bodemniveau
• Alle extra knopen (> k) zitten op het hoogste niveau.
• Knopen met een hoger nummer worden hoger geplaatst. Dit noemen we een bushvorm. In de onderstaande figuur zien we een bushform. Daarbij begint de uitleg van wat er gebeurt als een knoop wordt ingevoegd.

Wat gebeurt er als we een knoop toevoegen?

• Alle pijlen naar die knoop moeten "naast elkaar" komen te staan:



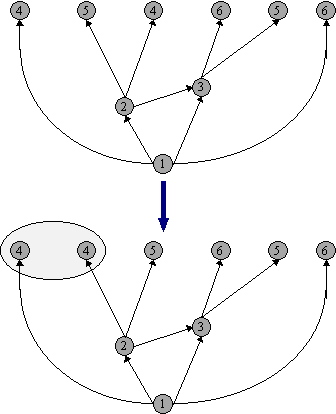
• De knoop wordt ingevoegd:



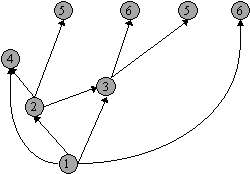
• Nieuwe uitgaande pijlen worden getrokken:



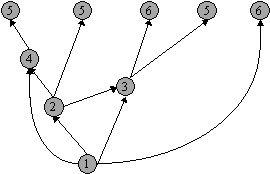
• En verder:





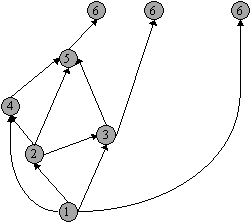
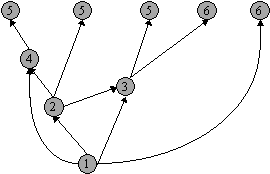
• Uiteindelijk krijgen we dus:



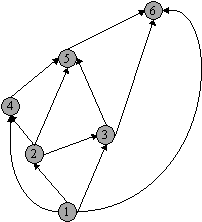
In feite is de bushvorm een inbedding van G_k, en vanwege Lemma 6 weten we dat we inderdaad er voor kunnen zorgen dat uitgaande pijlen naar de laagst genummerde nog niet getekende knoop naast elkaar kunnen komen te staan. We kunnen de bushvorm op de volgende manier veranderen:



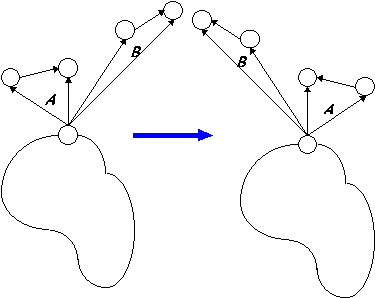
• Bij een separatieknoop kunnen de hoger gelegen componenten onderling gepermuteerd worden:
• Een biconnected component kan in vertikale richting worden gespiegeld:



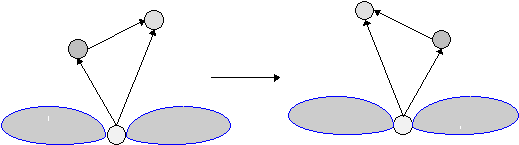
• De uitgaande extra pijlen bij een knoop kunnen gepermuteerd worden (dit is net zoals bij het 1^e geval).





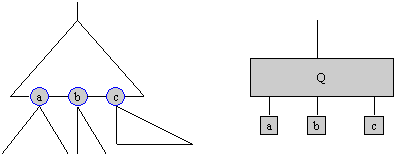
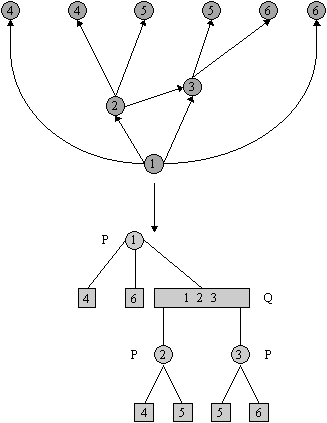
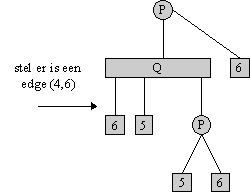
Nu representeren we de bushvorm als volgt:

• Iedere biconnected component van G_k is een Q-knoop.
• Iedere separatieknoop of knoop die extra kanten heeft is een P-knoop.
• De wortel is de component die knoop 1 bevat.
• Maak een kant tussen P-knoop en Q-knoop als de betreffende separatieknoop tot de biconnected component behoort.
• De volgorde van knopen op een Q-knoop is de volgorde waarin de separatieknopen op de buitenkant van de component verschijnen (zie figuur).

Bij het invoegen van knoop I:

• Laat S de verzameling kanten naar I zijn.
• Voer Reduce(S, T) uit Þ forceer dat alle kanten naar i naast elkaar komen te zitten.
• Laat alle bladeren naar i toe weg uit de PQ-boom, en zet op die plek alle kanten/bladeren die van i uitgaan (met daarboven een P-knoop, indien er meerdere van dat soort kanten zijn).







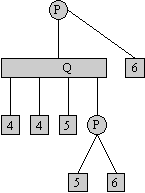
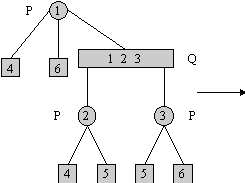
De resulterende PQ-boom weerspiegeld weer het buitenvlak van G. De tijd die het algoritme kost: O(V).