Waar is x gebleven?

Tegenwoordig werken leerlingen in de brugklas met taxi-tarieven en bedragen die gespaard worden. Wat heeft dat met grafieken en algebra te maken?

Hoofdrekenen gaat vooraf aan cijferend vermenigvuldigen en delen. Met het hoofdrekenen ontwikkel je namelijk inzicht in getallen en getalsystemen. Dat inzicht is nodig om te begrijpen wat er gebeurt als je berekeningen maakt via een standaardmethode. Zo gaat ook inzicht in formules en grafieken vooraf aan het oplossen van vergelijkingen. Tegenwoordig wordt veel aandacht besteed aan de ontwikkeling van dat inzicht vanuit praktische, herkenbare problemen. Zo kunnen leerlingen die inzichten ontwikkelen vanuit kennis die ze al hebben en zien ze direct de toepassingen ervan.

lineaire functies

Hieronder staat, wiskundig gezien, tweemaal hetzelfde probleem:

 

Opgave nu
Opgave vroeger

Peter heeft een klein bedrijf als klusjesman. Hij rekent _ 10 voorrijkosten en _ 45 per uur. Zijn collega Arnold rekent _ 70 voorrijkosten en _ 30 per uur.

Vanaf welk aantal uren is het voordeliger om Arnold te vragen voor een klus?

 

Voor welke waarde(n) van x geldt:

30x + 70 < 45x + 10

 

Leerlingen krijgen eerst een aantal praktische problemen zoals die van de klusjesmannen. Ze lossen die problemen op door te redeneren met de gegevens in de situatie.

 

Nu eerst redeneren
Vroeger direct een standaard methode

 

Arnold rekent _ 60 meer voorrijkosten. Maar het uurloon van Arnold is _ 15 meer. Dus na 4 uur heb je dat verschil er uit want 4 x 15 = 60. Daarna is Arnold voordeliger.

 

oplossing: bij een klus die meer dan 4 uur duurt is Arnold voordeliger

1e stap: breng 45x naar links

- 15x + 70 < 10

2e stap: breng 70 naar rechts

- 15x < - 60

3e stap: delen door - 15, het teken `klapt om'

x > 4

 

oplossing: x > 4 met x ∈ ℜ

 

Na een tijdje zien ze dat het bij al die opgaven telkens gaat om een formule met een vaste hoeveelheid van iets waarna er met elke stap (week, uur) eenzelfde hoeveelheid bij komt of af gaat. Dan hebben ze kunnen generaliseren en geleerd dat alle functies van die vorm eerstegraads functies heten. Dat is wiskunde: het herkennen en aanbrengen van structuren, zodat je het gemeenschappelijke in situaties ziet en met een algemene methode problemen eenvoudiger kunt oplossen.

In plaats van de woordformule totale kosten = 70 + 30 x aantal uren leren leerlingen dan pas de vorm met x en y, zoals y = 30 x + 70. Snijpunten van grafieken berekenen betekent dan: wanneer rekenen Peter en Arnold hetzelfde bedrag voor een klus? Welke waarde van x is de oplossing van de vergelijking 30x + 70 = 45x + 10 ?

Wanneer je alleen maar de formele oplossingen leert te maken, oefen je waarschijnlijk alleen maar een `trucje' dat je ook weer gemakkelijk vergeet. Als je betrokken bent bij het ontwikkelen van een algemeen model dat verband houdt met een hele serie verschillende situaties, dan heb je wiskunde gedaan en geleerd.

Grafieken van lineaire functies

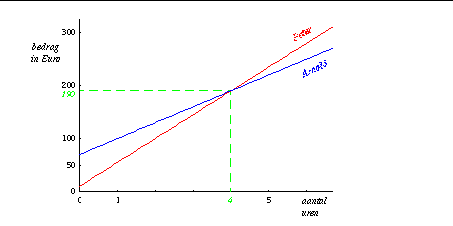
Hieronder staan de grafieken van de tarieven van Arnold en Peter. In de grafieken is ook te zien dat ieder uur bij elk tarief er een vast bedrag bij komt. Daardoor zijn het rechte lijnen en is de grafiek van Peter (45 Euro per uur) steiler dan die van Arnold (30 Euro per uur).

 

 

Het oefenen van de samenhang tussen eerste graads functies en hun grafieken kan tegenwoordig ook op een speels manier met het programma Bollen schieten.

 

Dit programma komt van het Wisweb. Naast allerlei andere programma's (applets genaamd) is daar ook meer informatie over het gebruik van Bollen schieten in de klas te vinden.