Almagest Ephemeris Calculator
Note: This web page is best viewed with a minimum
horizontal screen size of 1000 pixels.
The astronomer Claudius Ptolemy.
Sculpture in the Münster of Ulm by Jörg Syrlin the Elder (c. 1470).
 |
|
This web page provides a set of JavaScript calendar and
ephemeris modules for calculating geocentric luni-solar and planetary positions
for an arbitrary calendar date according to the kinematical models of the sun,
the moon and the planets described in the
Mathematike Syntaxis (better known from the title of the later
Arabic/Latin translations as the Almagest) of Claudius Ptolemy of Alexandria (c. 150 CE).
The mean motions of the sun, the moon and the planets adopted
in the Almagest Ephemeris Calculator correspond exactly with Ptolemy’s mean
motion tables and the corrections for their eccentric and epicyclical motions
are modelled according to the luni-solar and planetary models discussed by
Ptolemy in his Almagest.
As Ptolemy’s tables were probably used most often for
astrological rather than for astronomical computations, a table displaying the
astrological aspects between the luminaries (and the lunar ascending node) with
some other astrological quantities is also provided.
When the web page is loaded the Almagest Ephemeris Calculator
automatically selects the epoch date for the tables in Ptolemy’s Almagest
as the default date. This corresponds approximately with apparent noon (solar
time) at the meridian of Alexandria on 1 Thoth, 1 Nabonassar (or 26 February,
747 BCE, in the proleptic Julian calendar, around 9h 42½m UT).
Other dates and times can be inputted directly in the
calendar date module (at present only in the ‘mobile’ Egyptian calendar)
or can be set with an auxiliary module that allows for time adjustments in steps
ranging from 1-second to 100-year intervals.
It is also possible to adjust the time with the following
calendrical units:
- 1 mean lunation (29;31,50,8,20d)
- 1 regular lunar year = 12 mean lunations (354;22,1,40d)
- 1 embolistic lunar year = 13 mean lunations (383;53,51,48,20d)
- 1 tropical year (365;14,48d)
- 1 Metonic cycle = 235 mean lunations (6939;41,22,38,20d)
- 1 mean Jupiter-Saturn conjunction (7253;6,28,6,58,25,45d)
The tables in the Almagest are based on the ancient
version of the Egyptian calendar with a constant year length of 365 days and no
intercalary days. The epoch of the tables is fixed at the first year of the
reign of the Babylonian king
Nabu-nasir
(Nabonassar, reigned 747-734 BCE) as this predated the earliest (Babylonian)
observations that were available to Ptolemy (cf. Almagest III 7).
Compared with the Julian calendar, the dates in this calendar shift one day in
every four years and it is therefore often referred to as the ‘mobile’ or
‘wandering’ Egyptian calendar.
Ptolemy makes no reference in the Almagest to the more
modern version of the Egyptian calendar that was introduced in 26 BCE (or
30 BCE, as some sources suggest) by the Roman emperor Augustus. This calendar,
commonly referred to as the Alexandrian or ‘fixed’ Egyptian calendar, remained
in step with the Julian calendar (introduced in the Roman Empire in 45 BCE by
Julius Caesar) by inserting an intercalary day (a 6th epagomenal day) every four
years at the end of the year preceding the Roman year that contained the Julian
leap day. Although no use was made of the Alexandrian calendar in the
Almagest, a provision for converting to this calendar is included as it was
commonly used by later Hellenistic astronomers and astrologers.
In Ptolemy’s time the Egyptian calendar day started at dawn
(about one to two nocturnal hours before sunrise)
and noon was defined as 6 diurnal hours after sunrise. Likewise, sunset occurred
12 diurnal hours after sunrise with midnight occurring 6 nocturnal hours later.
However, as the lengths of diurnal and nocturnal hours depend both on the
observer’s latitude as on the season, they are not convenient for astronomical
calculations.
Ptolemy therefore adopted hours of equal length (also known as
equinoctial hours) in his tables and shifted the epoch from dawn to mean
local noon (6 hours) at the meridian of Alexandria. Sunrise, as measured in
equal hours, will then on average occur about 6 equal hours earlier but the
exact value will depend on the season. Sunset, likewise, will on average occur
about 6 equal hours after noon but the exact value will again depend on the
season.
Note that dates between sunset and sunrise are commonly
indicated in the Almagest as a double date (the first referring to the
current day, the second to the day starting after the next sunrise). For the
conversion from Alexandria mean local time to Universal Time (Greenwich Mean
Time), a longitude difference of exactly 30º 0' 0" between Alexandria and
Greenwich has been adopted. A negative offset of 17m 34s has been introduced to
correct for the difference between Ptolemy’s “equation of time” and its modern
definition (see below).
Note that both the Julian as the
Alexandrian calendars are here represented in their ‘ideal’ (or proleptic)
forms and do not implement the incorrect use of Julius Caesar’s quadrennial
leap year rule before 8 CE. For details on the actual use of these calendars
in Egypt during the reign of Augustus, cf. Snyder (1943) and Skeat (1993,
2001) – for an alternative view, cf. Hagedorn (1994) and Jones (2000).
The zodiacal calendar of Dionysius,
an otherwise unknown astronomer who observed in Alexandria in the second
quarter of the third century BCE, in the calendar module is based on the
reconstruction of Böckh (1863) and Van der Waerden (1984). It assumes a
solar year of 365 days with a leap day at the end of the third year of
each four-year cycle. Each month is assumed to be 30 days in length and
is named after the zodiacal sign traversed by the sun during most of
that month. The first year of the zodiacal calendar of Dionysius is
assumed to start on 26 June 285 BCE, at sunrise, and largely overlaps
the first regnal year of Ptolemy Philadelphus.
The calendar module also provides a
tentative conversion to the Greek astronomical calendar of Callippus as
described by Geminus (Elementa astronomiae VIII.50-60) and often
referred to in the
Almagest. The conversion is based on a reconstruction of this
arithmetical luni-solar calendar from the data in the Almagest by
Fotheringham (1924) and Van der Waerden (1960, 1984), with additional
constraints derived from other sources by Jones (2000). It assumes that
in every 76-year cycle each 64th day is omitted (as well as the last day
at the end of the cycle) and that seven years in each 19-year Metonic
sub-cycle have an intercalated month (Poseideon II in the years 1, 6 &
14, and Skirophorion II in the years 3, 9, 11 & 17).
The Callippic calendar is assumed to
commence on 28 June 330 BCE, at sunset following the new moon after the
summer solstice following Alexander the Great’s conquest of Babylon.
Other reconstruction schemes are also possible but this appears to be
the simplest one that satisfies nearly all known Callippic dates. Both
the Dionysian as the Callippic date converters should be used with
caution but they may be useful in identifying new Dionysian or Callippic
dates which in turn can help to refine our incomplete knowledge on these
astronomical calendars. |
The equation of time, a correction factor necessary for
converting apparent solar time into mean solar time was already recognized by
Ptolemy (Almagest III.9). As the correction is negligible for slow-moving
luminaries, Ptolemy only applies it to the fastest-moving luminary (the moon).
Ptolemy’s equation of time as function
of the mean solar longitude
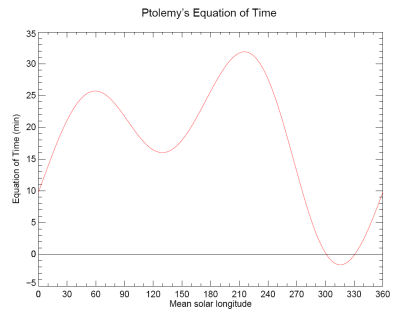 |
|
In Ptolemy’s luni-solar and planetary tables the equation of
time is defined to be zero at the epoch of the tables (1 Thoth, 1 Nabonassar).
The consequence of this choice is that during most of the year the equation of
time has a positive value (small negative values only occur when the mean
longitude of the sun is between 301.02º and 330.75º).
Ptolemy’s definition for the equation of time was commonly
used by astronomers up the late 17th century after when it was replaced by the
modern definition resulting in positive and negative values which are equally
distributed in the year.
In the Almagest Ephemeris Calculator the correction for the
equation of time can be applied to all luminaries by selecting the appropriate
mode in the calendar date module
(the default mode is ‘off’,
i.e. the time for Alexandria is assumed to given in mean solar time).
Ptolemy’s astronomical tables are based on the meridian of
Alexandria (referred to by Ptolemy as the “Metropolis of all Egypt”).
For conversion to other ancient astronomical prime meridians,
contemporary astronomers would have used contemporary estimates for their
longitude difference with Alexandria. The most comprehensive and authoritative
compilation of geographical longitudes and latitudes in antiquity was also
compiled by Ptolemy and is commonly known as the Geographica.
The following table lists some well-known ancient cities that
have functioned as astronomical meridians in the past with their geographical
longitudes and inferred time offsets relative to Alexandria as tabulated in
Ptolemy’s Geographica.
Ancient Astronomical
Prime Meridians
| Location |
Longitude |
Time offset |
Ref. |
| Babylon |
79º |
+1h 14m |
V 20.6 |
| Jerusalem (Hierosolyma) |
66º |
+0h 22m |
V 16.8 |
| Alexandria |
60;30º |
+0h 00m |
IV 5.9 |
|
Constantinople (Byzantium) |
56º |
–0h 18m |
III 11.5 |
| Athens |
52;45º |
–0h 31m |
III 15.22 |
| Rome |
36;40º |
–1h 35m |
III 1.61 |
Note that Ptolemy’s geographical longitudes are measured
eastwards from the “Fortunate Isles”, the westernmost habitable region of the
world known at that time, which are commonly identified with the Canary Islands.
In the near future, a complete online version of Ptolemy’s
Geographica will be available at Bill Thayer’s website
Ptolemy: The Geography.
The Almagest Ephemeris Calculator can also be used for
predicting the date and time (to the nearest second if desired, although this
accuracy was unattainable with the time-measuring devices then available) of the
astronomical seasons, the lunar phases (syzygies), planetary stations (when a
planet’s motion in longitude changes from direct to retrograde or from
retrograde to direct) and planetary aspects such as conjunctions or oppositions
between any pair of planets.
For instance, to determine the date of the vernal equinox
(when the true solar longitude is 0º) for a given year, input a first estimate
(say 25 March, the traditional date in Julius Caesar’s solar calendar) for the
date in the calendar date module
and click for the solar position module.
This results in a true solar longitude value close to 360º/0º. Adjust the time
(only the ±1-day and smaller time interval buttons will be necessary) until the
true solar longitude is as close to 0º as you want it to be. Return to the
calendar date module to obtain the predicted calendar date and time
(referred to the meridian of Alexandria) for the vernal equinox of that year.
Likewise, the dates of the other astronomical seasons can be
derived by homing in to a true solar longitude of 90º (summer solstice), 180º
(autumnal equinox) or 270º (winter solstice). For lunar phases, go to the
lunar position module (after inputting a first estimate in the
calendar date module) and home in to a true luni-solar elongation of 0º
(new moon), 90º (first quarter), 180º (full moon) or 270º (last quarter).
For planetary stations and planetary aspects, go to the luni-solar and planetary aspect module and follow similar
procedures. The latter module can also be used to determine when the sun, the
moon or a planet enters or leaves a specific zodiacal sign (or one of its
smaller astrological partitions) .
Angular quantities calculated by the Almagest Ephemeris
Calculator are expressed in sexagesimal notation (this is indicated by the use
of a semicolon (;) separating the integer number of degrees from its sexagesimal
parts). Degrees, minutes and seconds are thus expressed as dd;mm,ss.
The Almagest only provides geocentric distances for the
sun and the moon. The geocentric distances to the other planets are based on the
radii of the planetary deferents and epicycles listed in Ptolemy’s Planetary
Hypotheses. The geocentric distances are also expressed in sexagesimal
notation.
Certain parameters in Ptolemy’s Almagest, such as the
obliquity of the ecliptic and the longitude of the solar apogee, are assumed to
be constant in time. This is indicated by outputting these parameters in
red. The values outputted in
green
are still provisional and need to be checked.
In order to obviate the necessity of including bulky
double-argument tables for correcting the mean positions of the moon and the
planets to their true positions, Ptolemy introduced some simplifications that
made it possible to considerably compress the size of the correction tables in
the Almagest. The results obtained from the Almagest Ephemeris Calculator
will therefore slightly deviate from the results obtained directly from
Ptolemy’s tables but the difference will never amount to more than a few minutes
of arc.
The mathematical representations of Ptolemy’s kinematical
models used in the Almagest Ephemeris Calculator are explained in detail in
various publications listed in the bibliography: especially useful in this respect are the
works of Neugebauer (1957, 1975), Pedersen (1974), North (1976), Evans (1998)
and Jacobsen (1999).
Click here for the
precession in longitude and obliquity of the ecliptic, the position of
the sun, the
moon, the planets
Mercury, Venus, Mars, Jupiter, Saturn
or a table listing the
luni-solar and planetary aspects.
Return to the
calendar date module.
Return to the
calendar date module.
Return to the
calendar date module.
Return to the
calendar date module.
Return to the calendar
date module.
Return to the calendar
date module.
Return to the calendar
date module.
Return to the calendar
date module.
Return to the calendar
date module.
Aspects and orbs of influence
The above table lists the aspects (based on a 2-, 3-, 4- and
6-fold division of the ecliptic circle) that are commonly encountered in
classical, Islamic and medieval astrological texts:
- Conjunction – angular separation 0º.
- Sextile – angular separation 60º.
- Quartile (square) – angular separation 90º.
- Trine – angular separation 120º.
- Opposition – angular separation 180º.
According to Greek and later Islamic astrological traditions a
luminary is considered to be “tashriq” or “under the rays” of the sun when its
angular distance from the sun’s centre is:
- 12° for the moon, Mercury and Venus.
- 15° for Jupiter and Saturn.
- 18° for Mars.
Within 0;16º of the sun’s centre a luminary is termed
“cazimi”, derived from the later Arabic term indicating that it is in the
“heart” of the sun, and up to 6º from the sun’s centre a luminary is termed
“combust”.
The lower left half of the first table lists the aspects while
the angular differences (in degrees and decimal parts) in ecliptic longitude are
tabulated in the upper right half of the table.
Signs and sign rulers
The second table lists the sign and degree within the sign for
each luminary with some further astrological quantities. The zodiacal signs are
abbreviated as follows: Ari = Aries, Tau = Taurus, Gem = Gemini, Cnc = Cancer,
Leo = Leo, Vir = Virgo, Lib = Libra, Sco = Scorpius, Sgr = Sagittarius, Cap =
Capricornus, Aqr = Aquarius and Psc = Pisces.
The “sign ruler” (also known as the “domicile lord”) is the
planet that is traditionally assigned to rule over each of the signs: Saturn is
said to rule over Capricornus and Aquarius, Jupiter over Sagittarius and Pisces,
Mars over Aries and Scorpius, the sun over Leo, Venus over Taurus and Libra,
Mercury over Gemini and Virgo and finally, the moon over Cancer.
Tropical versus sidereal longitudes
Ptolemy’s ecliptic longitudes are measured with respect to the
First Point of Aries (i.e.
the place occupied by the sun at the vernal equinox) and are therefore known as
tropical longitudes. According to Ptolemy, the Greek astronomer Hipparchus
of Nicaea (c. 150 BCE) discovered that this point (0º Aries) slowly
shifts westwards with respect to the fixed stars. The rate of the precession of
the equinoxes, as it is commonly called, was estimated by Ptolemy to be about 1º
in 100 Egyptian years.
Theon of Alexandria (Small Commentary on Ptolemy’s Handy
Tables 12) mentions a tradition of “ancient astrologers” to measure ecliptic
longitudes from a reference point that oscillated 8º backwards and forwards with
respect to the stars. Some 128 years before the reign of the Roman emperor
Augustus (i.e. around 158 BCE), this reference point was supposed to be
at its farthest limit 8º away from the (tropical) First Point of Aries but since
then it was assumed to be moving towards it at a rate of 1º in every 80 Egyptian
years. From Theon’s description one can infer that after its coincidence with
the (tropical) First Point of Aries (which would occur in 483 CE, long after
Theon’s time), this reference point was believed to reverse in direction again
and move away from it at the same rate, thus repeating its backward and forward
motions in a 1280-year cycle.
Though the sidereal longitude system is supported here (it is
often encountered in Greek astrological papyri), the tropical longitude system
is chosen as default as this was the system that was used by Ptolemy (and
recommended by Theon of Alexandria) for astronomical calculations.
Decan rulers
The “decans” are divisions (of Egyptian origin) of each
zodiacal sign into three 10º sections, each of which is associated with a
planetary ruler (“prosopa” or “planetary face”). According to Firmicus Maternus
(Mathesis II.4) and Paulus of Alexandria (Isagoge 4) the sequence
of decan rulers follows the traditional sequence of the planets (Saturn,
Jupiter, Mars, sun, Venus, Mercury, moon), starting with Mars as the ruler of
the first decan of Aries and ending with Mars as the ruler of the last decan of
Pisces.
Term rulers
The “terms” are sections of unequal lengths dividing the
zodiacal signs, each of which are ruled by one of the five star-like planets
(thus excluding the sun and the moon). Ptolemy describes three such pentazone
systems in his Tetrabiblos (I.20-21): one attributed to the “Chaldeans” (i.e.
Babylonians), one to the “Egyptians” (probably referring to the 2nd-century BCE
astrologers Nechepso and Petosiris) and one attributed to an “ancient
manuscript”. The latter system is now commonly known as Ptolemy’s system.
A variant system by Vettius Valens (Anthologiae
III.6[9]) also assigns terms in each sign to the sun and the moon. Note that
both the Chaldean system as the heptazone system of Vettius Valens distinguish
between day- and night-time term rulers. In the Chaldean system the planets
Mercury and Saturn switch positions depending on whether the sun is above or
below the horizon: in the system of Vettius Valens the planets Venus and Jupiter
also switch positions with those of the moon and the sun.
Ptolemy’s pentazone system is also mentioned by Vettius Valens
(Anthologiae
I.3), who, however, gives different lengths and rulers for the terms of Libra.
The aspect module adopts the Egyptian system as default as this was the most
commonly used system in the Greek horoscopes that are known to us.
Monomoiria
The “monomoiria” are the planets associated with each degree
of the zodiac. Of the various monomoiria systems described in the astrological
literature, the system of Vettius Valens (Anthologiae IV.26) has been
implemented in the aspect module (cf. Neugebauer & van Hoesen, 1959, p. 10).
Ptolemy’s triquetrum (or ‘parallactic
instrument’) according to William Cunningham’s The Cosmographical
Glasse, conteinyng the Pleasant Principles of Cosmographie, Geographie,
Hydrographie, or Navigation (London: John Day, 1559)
 |
|
Editions and Translations of the Almagest
- Georg von Peuerbach & Regiomontanus, Johannes, Epytoma Joãnis de Mõte Regio in Almagestũ ptolomei ([Nuremberg]: Johannes Hamman de
Landoia, 1496) [E-RARA link /
Gallica link] – paraphrase,
largely based the Latin translation made by Gerard of Cremona from the Arabic
in 1175, lacking the tables and the star catalogue.
- Almagestum Cl. Ptolemaei Pheludiensis Alexandrini, astronomorum principis, opus ingens ac nobile, omnes coelorum motus continens
(Venice: Petrus Lichtenstein, 1515) [E-RARA link] – based on
the Latin translation from the Arabic made in 1175 by Gerard of Cremona.
- Cl. Ptolemaei Pheludiensis Alexandrini Almagestum seu Magnae Constructionis Mathematicae opus plane divinum Latina donatum lingua ab
Georgio Trapezuntio usquequaque doctissimo, per Lucam Gauricum, Neap. divinae matheseos prof. egregium (Venice: Giunti, 1528);
reprinted in 1541 (Hieronymus Gemusäus, Basle) and 1551 (Oswald Schrekenfuchs, Basle) – based on the Latin translation from the Greek made
in 1451 by Georgius of Trebizond; with a foreword by Luca Gaurica.
- Grynaeus, Simon, Claudii Ptolemaei Magnae Constructionis, id est Perfectae coelestium motuum pertractionis, Libri XIII (Basle:
Johannes Walder, 1538) [E-RARA link] – published with Theon
of Alexandria’s commentary on the Almagest (edited by Joachim Camerarius); both editions were based on Greek manuscripts formerly owned by
Johannes Bessarion and (later) by Johannes Regiomontanus.
- Gemusaeus, Hieronymus, Clavdii Ptolemaei Pelvsiensis Alexandrini Omnia, vae Extant, Opera, Geographia excepta, quam seorsim quoq[ue]
hac forma impressimus. [...] Ex, in omnibus disciplinis principum uirorum, exemplaribus emendauimus Almagesti plurima loca & figuras
nonnullas, quas sculptas in primo huius operis limine posuimus, quoniam magnam lucem uidebantur allatur[a]e rebus sua natura obscurioribus.
Ob qua[m] causam etiam censuimus addendas Luc[a]e Gaurici annotationes. Item omnium constellationum figuras graphice, propter singulare
studiosorum co[m]modum, depinximus (Basle: Heinrich Petri, 1541)
[JALB link] – Latin translation.
- Halma, Nicholas B., Composition mathématique de Claude Ptolémée: Tome premier (Paris: Henri Grand, 1813)
[Gallica link].
- Halma, Nicholas B., Composition mathématique de Claude Ptolémée, ou astronomie ancienne: Tome second (Paris: J.-M. Eberhart,
1816) [Gallica link].
- Heiberg, Johan Ludvig, Claudii Ptolemaei Opera quae exstant omnia: I. Syntaxis mathematica. Pars I (Leipzig: B.G. Teubner
Verlag, 1898 [= Bibliotheca scriptorum graecorum et romanorum teubneriana])
[Internet Archive link /
Thesaurus Linguae Graecae link].
- Heiberg, Johan Ludvig, Claudii Ptolemaei Opera quae exstant omnia: I. Syntaxis mathematica. Pars II (Leipzig: B.G. Teubner
Verlag, 1903 [= Bibliotheca scriptorum graecorum et romanorum teubneriana]) [Thesaurus
Linguae Graecae link].
- Manitius, Karl, Des Claudius Ptolemäus: Handbuch der Astronomie. Erster Band (Leipzig: B.G. Teubner Verlag, 1912)
[Internet Archive link] – reprinted with an
introduction by Otto E. Neugebauer in 1963 (B.G. Teubner Verlagsgesellschaft, Leipzig).
- Manitius, Karl, Des Claudius Ptolemäus: Handbuch der Astronomie. Zweiter Band (Leipzig: B.G. Teubner Verlag, 1913)
[Internet Archive link] – reprinted with an
introduction by Otto E. Neugebauer in 1963 (B.G. Teubner Verlagsgesellschaft, Leipzig).
- Taliaferro, Robert Catesby, The Almagest, by Ptolemy, in: M.J. Adler, C. Fadiman & Ph.W. Goetz (eds.),
The Great Books of the Western World: Vol. 16 (Chicago: Encyclopaedia Britannica, 1952) – vol. 15 of the 1990 reprint.
- Toomer, Gerald J., Ptolemy’s Almagest (London: Duckworth, 1984 [= Duckworth Classical, Medieval and Renaissance Editions]) –
reprinted in 1998 with a foreword by Owen Gingerich by Princeton University Press (Princeton).
- Veselovskij, Ivan Nikolaevich, Klavdij Ptolemej Al’magest: Ili Matematiěskoe Sočinenie v Trinadcati Knigach (Moscow: Nauka Fizmatlit,
1998).
Studies on the Kinematical Models of the Almagest
- Delambre, Jean-Baptiste Joseph, Histoire de l'astronomie ancienne (Paris: Mme Ve Courcier, 1817), vol. 2
[Internet Archive link].
- Kempf, Paul Friedrich Ferdinand, Untersuchungen über die Ptolemäische Theorie der Mondbewegung (Berlin: A.W. Schade's
Buchdruckerei, 1878).
- Oudemans, Jean Abraham Chrétien, “Het problema van Snellius, opgelost door Ptolemaeus”, Verslagen en Mededeelingen der Koninklijke
Akademie van Wetenschappen: Afdeeling Natuurkunde, Tweede Reeks, 19 (1884), 436-441
[Internet Archive link] – also
published in German as: “Lösung des sog. Pothenot'schen, besser Snellius'schen Problems von Ptolemaeus”, Vierteljahrsschrift
der Astronomischen Gesellschaft, 22 (1887), 345-349 [Internet Archive link].
- Coolhaas, Gerrit Jan Marie, De theorie van de beweging der Maan vóór Newton (Utrecht: Van der Post, 1884)
[ULU link].
- Herz, Norbert, Geschichte der Bahnbestimmung von Planeten und Kometen. I. Theil: Die Theorien des Alterthums (Leipzig:
B.G. Teubner Verlag, 1887) [GDZ link].
- Bouché-Leclercq, Auguste, l’Astrologie grecque (Paris: E. Leroux, 1899).
- Lynn, William Thynne, “Hipparchus and the Precession of the Equinoxes”, The Observatory, 27 (1904) 347
[ADS link].
- Boelk, Paul Ferdinand Wilhelm, Darstellung und Prüfung der Mercurtheorie des Claudius Ptolemaeus (Göttingen: Kästner, 1911).
- Schumacher, Carl Heinrich Josef, Untersuchungen über die ptolemäische Theorie der unteren Planeten (Merkur und Venus) (Münster in
Westfalen: Aschendorffschen Verlagsbuchhandlung, 1917).
- Rome, Adolphe, “Le troisième livre des commentaires sur l'Almageste, par Théon et Hypatie”, Annales de la Société Scientifique de
Bruxelles, Série A, 46 (1926), 1-14 – reprinted in Publications du Laboratoire d'Astronomie et de Géodésie de
l'Université de Louvain, 3 (1926), 9-22 [ADS link].
- Rome, Adolphe, “L'astrolabe et le météoscope d'après le commentaire de Pappus sur le 5e livre de l'Almageste”,
Annales de la Société Scientifique de Bruxelles, Série A, 47 (1927), 77-101 – reprinted in Publications
du Laboratoire d'Astronomie et de Géodésie de l'Université de Louvain, 4 (1927), 125-149
[ADS link].
- Rome, Adolphe, “L'instrument parallactique d'après le commentaire de Pappus sur le 5e livre de l'Almageste”,
Annales de la Société Scientifique de Bruxelles, Série A, 47 (1927), 129-140 – reprinted in Publications
du Laboratoire d'Astronomie et de Géodésie de l'Université de Louvain, 4 (1927), 247-258
[ADS link].
- Rome, Adolphe, “Les observations d'équinoxes et de solstices dans les chapitre 1 du livre 3 du Commentaire sur
l'Almageste par Théon d'Alexandrie”, Annales de la Société Scientifique de Bruxelles, Série 1, 57 (1937),
213-236 & 58 (1938), 6-26 – summarized as “Les observations d'équinoxes de Ptolémée”, Ciel et Terre:
Bulletin de la Société Belge d'Astronomie, de Météorologie et de Physique du Globe, 59 (1943), 141-155
[ADS link].
- Rome, Adolphe, “Le problème de l’équation du temps chez Ptolémée”, Annales de la Société Scientifique de Bruxelles,
Série 1, 59 (1939), 211-224.
- Pannekoek, Anton, “The Planetary Theory of Ptolemy”, Popular Astronomy: A Review of Astronomy and Allied Sciences,
55 (1947), 459-476 [ADS link].
- Neugebauer, Otto E., “Mathematical Methods in Ancient Astronomy”, Bulletin of the American Mathematical Society, 54
(1948), 1013--1041 [AMS link] ‒
reprinted in: O.E. Neugebauer, Astronomy and History: Selected Essays (New York: Springer, 1983), pp. 99-127.
- Rome, Adolphe, “La prosneuse des éclipses dans l'astronomie Ptolémaïque: Note préliminaire”, L'antiquité classique,
17 (1948), 509-518.
- Chatterjee, Bina, “Geometrical Interpretation of the Motion of the Sun, Moon and the Five Planets as found in the Mathematical
Syntaxis of Ptolemy and in the Hindu Astronomical Works”, Journal of the Royal Asiatic Society [Bengal Branch], 15
(1949), nr. 2, 41-89.
- Michel, Henri, “Sur l’origine de la théorie de la trépidation”, Ciel et Terre: Bulletin de la Société Belge d’Astronomie,
de Météorologie et de Physique du Globe, 66 (1950), 227-234 [ADS link].
- Pannekoek, Anton, “Ptolemy’s Precession”, Vistas in Astronomy, 1 (1955), 60-66
[ScienceDirect link].
- Hartner, Willy, “The Mercury Horoscope of Marcantonio Michiel of Venice: A Study in the History of Renaissance Astrology and
Astronomy”, Vistas in Astronomy, 1 (1955), 84-138 [ScienceDirect link] – reprinted (with minor corrections) in W. Hartner, Oriens-Occidens: Ausgewählte
Schriften zur Wissenschafts- und Kulturgeschichte. Festschrift zum 60. Geburtstag (Hildesheim: Georg Olms
Verlagsbuchhandlung, 1968), pp. 440-495.
- Stumpff, Karl, Himmelsmechanik (Berlin: VEB Deutscher Verlag der Wissenschaften, 1958 [= Hochschulbücher für
Physik, Band 32]), Band I, Kapitel I.
- Neugebauer, Otto E. & van Hoesen, Henry Bartlett, Greek Horoscopes (Philadelphia: American Philosophical Society,
1959 [= Memoirs of the American Philosophical Society, nr. 48]).
- Hanson, Norwood Russell, “The Mathematical Power of Epicyclical Astronomy”, Isis: An International Review devoted to the
History of Science and its Cultural Influences, 51 (1960), 150-158 [JSTOR link].
- Goldstein, Bernard R., “On the Theory of Trepidation”, Centaurus: International Magazine of the History of Science and
Medicine, 10 (1964/65), 232-247 [Wiley link].
- Goldstein, Bernard R., The Arabic Version of Ptolemy’s Planetary Hypotheses (Philadelphia: American Philosophical
Society, 1967 [= Transactions of the American Philosophical Society, 57, nr. 4])
[JSTOR link].
- Petersen, Viggo M. & Schmidt, Olaf, “The Determination of the Longitude of the Apogee of the Orbit of the Sun according
to Hipparchus and Ptolemy”, Centaurus: International Magazine of the History of Science and Medicine,
12 (1968), 73-96 [Wiley
link].
- Petersen, Viggo M., “The Three Lunar Models of Ptolemy”, Centaurus: International Magazine of the History of Science and
Medicine, 14 (1969), 142-171 [Wiley link].
- Swerdlow, Noel M. & Goldstein, Bernard R., “Planetary Distances and Sizes in an Anonymous Arabic Treatise preserved in
Bodleian ms. Marsh 621”, Centaurus: International Magazine of the History of Science and Medicine, 15
(1971), 135-170 [Wiley link].
- Gingerich, Owen, “The Mercury Theory from Antiquity to Kepler”, in: Actes du XIIe Congrès International d’Histoire des
Sciences, Paris, 1968 (Paris: Librairie Scientifique et Technique Albert Blanchard, 1971), vol. 3A, pp. 57-64 –
reprinted in O. Gingerich, The Eye of Heaven: Ptolemy, Copernicus, Kepler (New York: American Institute of Physics,
1993), pp. 379-387.
- Pedersen, Olaf, A Survey of the Almagest (Odense: Odense University Press, 1974 [= Acta Historica Scientiarum
Naturalium et Medicinalium, nr. 30]).
- Neugebauer, Otto E., A History of Ancient Mathematical Astronomy (Berlin [etc.]: Springer-Verlag, 1975 [=
Studies in the History of Mathematics and Physical Sciences, nr. 1]), 3 vols.
- Whiteside, Derek Thomas, “A Refined Computation of the Perigee Angle in Ptolemy’s Mercury Model”, Journal for the History
of Astronomy, 6 (1975), 57 [ADS link].
- North, John D., Richard of Wallingford (Oxford: Clarendon Press, 1976), 3 vols.
- Mercier, Raymond, “Studies in the Medieval Conception of Precession”, Archives Internationales d’Histoire des Sciences,
26 (1976), 197-220 & 27 (1977), 33-71 – reprinted in R. Mercier, Studies on the Transmission of Medieval
Mathematical Astronomy (Aldershot/Burlington: Ashgate/Variorum, 2004 [= Variorum Collected Studies Series, nr. CS787]),
nrs. IIa & IIb.
- Newton, Robert R., The Crime of Claudius Ptolemy (Baltimore/London: Johns Hopkins University Press, 1977).
- Riddell, R.C., “The Latitudes of Venus and Mercury in the Almagest”, Archive for History of Exact Sciences, 19 (1978),
95-111 [SpringerLink].
- Gingerich, Owen, “Was Ptolemy a Fraud?”, Quarterly Journal of the Royal Astronomical Society, 21 (1980), 253-266
[ADS link] – reprinted in O. Gingerich, The
Eye of Heaven: Ptolemy, Copernicus, Kepler (New York: American Institute of Physics, 1993), pp. 55-73.
- Gingerich, Owen, “Ptolemy Revisited: A Reply to R.R. Newton”, Quarterly Journal of the Royal Astronomical Society,
22 (1981), 40-44 [ADS link] – reprinted in
O. Gingerich, The Eye of Heaven: Ptolemy, Copernicus, Kepler (New York: American Institute of Physics, 1993),
pp. 74-80.
- Goldstein Jr., Samuel J., “Problems Raised by Ptolemy’s Lunar Tables”, Journal for the History of Astronomy, 13 (1982),
195-205 [ADS link] + errata, ibid., 15 (1984),
134-135 [ADS link].
- Gingerich, Owen, “Ptolemy and the Maverick Motion of Mercury”, Sky & Telescope, 66 (1983), 11-13
[ADS link] – reprinted in O. Gingerich,
The Great Copernicus Chase and Other Adventures in Astronomical History (Cambridge [Mass.]/Cambridge: Sky Publishing
Corporation/Cambridge University Press, 1992), pp. 31-35.
- Gingerich, Owen, “Ptolemy, Copernicus, and Kepler”, in: M.J. Adler & J. Van Doren (eds.), The Great Ideas Today 1983
(Chicago: Encyclopaedia Britannica, 1983), pp. 137-180 – reprinted in O. Gingerich, The Eye of Heaven: Ptolemy, Copernicus,
Kepler (New York: American Institute of Physics, 1993), pp. 3-51.
- Evans, James, “Fonction et origine probable du point équant de Ptolémée”, Revue de Histoire des Sciences, 37 (1984),
193-213 – published in English as: “On the Function and the Probable Origin of Ptolemy’s Equant”, American Journal of Physics,
52 (1984), 1080-1089 [AJP link].
- Hetherington, Norriss S. & Ronan, Colin A., “Ptolemy’s Almagest: Fourteen Centuries of Neglect”, Journal of the British
Astronomical Association, 94 (1984), 256-262 [ADS link].
- van der Waerden, Bartel Leendert, Die Astronomie der Griechen: Eine Einführung (Darmstadt: Wissenschaftliche Buchgesellschaft, 1988),
chapter XIX.
- Swerdlow, Noel M., “Ptolemy’s Theory of the Inferior Planets”, Journal for the History of Astronomy, 20 (1989), 29-60
[ADS link].
- Jones, Alexander R., “Hipparchus’s Computation of Solar Longitudes”, Journal for the History of Astronomy, 22 (1991), 101-125
[ADS link].
- Britton, John Phillips, Models and Precision: The Quality of Ptolemy's Observations and Parameters (New York/London: Garland
Publishing Inc., 1992 [= Sources and Studies in the History and Philosophy of Classical Science, nr. 1])
[Internet Archive link].
- Van Brummelen, Glen, Mathematical Tables in Ptolemy's Almagest (Burnaby: Simon Fraser University Department of Mathematics and
Statistics, 1993).
- Van Brummelen, Glen, “Lunar and Planetary Interpolation Tables in Ptolemy’s Almagest”, Journal for the History of Astronomy, 25
(1994), 297-311 [ADS link].
- van Dalen, Benno, “On Ptolemy’s Table for the Equation of Time”, Centaurus: International Magazine of the History of Science and
Medicine, 37 (1994), 97-153 [Wiley
link].
- Van Brummelen, Glen, “A Survey of the Mathematical Tables in Ptolemy’s Almagest”, in: A. von Gotstedter (ed.), Ad radices: Festband
zum fünfzigjährigen Bestehen des Instituts für Geschichte der Naturwissenschaften der Johann Wolfgang Goethe-Universität Frankfurt am Main
(Stuttgart: Franz Steiner Verlag, 1994), pp. 155-170.
- Nevalainen, J., “The Accuracy of the Ecliptic Longitude in Ptolemy’s Mercury Model”, Journal for the History of Astronomy, 27
(1996), 147-160 [ADS link].
- del Santo, Paulo & Strano, Giorgio, “Observational Evidence and the Evolution of Ptolemy’s Lunar Model”, Nuncius: Annali di Storia
della Scienza, 11 (1996), 93-122.
- Goldstein, Bernard R., “Saving the Phenomena: The Background to Ptolemy’s Planetary Theory”, Journal for the History of Astronomy,
28 (1997), 1-12 [ADS link].
- Van Brummelen, Glen, “Computer Animations of Ptolemy’s Models of the Motions of the Sun, Moon and Planets”, Journal for the History of
Astronomy, 29 (1998), 271-274 [ADS link].
- Evans, James, The History and Practice of Ancient Astronomy (Oxford: Oxford University Press, 1998).
- Jacobsen, Theodor S., Planetary Systems from the Ancient Greeks to Kepler (Washington: University of Washington Press, 1999).
- Savoie, Denis, “The Precession of the Equinoxes from Hipparchus to Tycho Brahe”, in: N. Capitaine (ed.), Journées 2000 – Systèmes
de références spatio-temporels: J2000, A Fundamental Epoch for Origins of Reference Systems and Astronomical Models (Paris:
Observatoire de Paris, 2000), pp. 125-130.
- Duke, Dennis W., “Computer Animations of Greek and Arabic Planetary Models”, Journal for the History of Astronomy, 35 (2004),
225-228 [ADS link].
- Sidoli, Nathan, Ptolemy's Mathematical Approach: Applied Mathematics in the Second Century (Toronto: University of Toronto Institute
for the History and Philosophy of Science and Technology, 2004).
- Swerdlow, Noel M., “The Empirical Foundations of Ptolemy’s Planetary Theory”, Journal for the History of Astronomy, 35 (2004),
249-271 [ADS link].
- Jones, Alexander, “A Route to the Ancient Discovery of Non-uniform Planetary Motion”, Journal for the History of Astronomy, 35
(2004), 375-386 [ADS link].
- Duke, Dennis W., “Ptolemy’s Treatment of the Outer Planets”, Archive for History of Exact Sciences, 59 (2005), 169-187
[SpringerLink].
- Duke, Dennis W., “Comment on the Origin of the Equant Papers by Evans, Swerdlow, and Jones”, Journal for the History of Astronomy,
36 (2005), 1-6 [ADS link].
- Swerdlow, Noel M., “Ptolemy’s Theories of the Latitude of the Planets in the Almagest, Handy Tables, and Planetary Hypotheses”, in:
J.Z. Buchwald & A. Franklin (eds.), Wrong for the Right Reasons (Berlin [etc.]: Springer, 2005 [= Archimedes:
New Studies in the History of Science and Technology, nr. 11]), pp. 41-71.
- Goldstein, Bernard R., “What’s New in Ptolemy’s Almagest?”, Nuncius: Journal of the History of Science, 22 (2007), 261-285.
- Jones, Alexander, “Ancient Rejection and Adoption of Ptolemy’s Frame of Reference for Longitudes”, in: A. Jones (ed.), Ptolemy in
Perspective: Use and Criticism of his Work from Antiquity to the Nineteenth Century (Berlin [etc.]: Springer, 2010 [= Archimedes:
New Studies in the History of Science and Technology, nr. 23]), pp. 11-44.
- Swerdlow, Noel M., “Tycho, Longomontanus, and Kepler on Ptolemy’s Solar Observations and Theory, Precession of the Equinoxes, and Obliquity
of the Ecliptic”, in: A. Jones (ed.), Ptolemy in Perspective: Use and Criticism of his Work from Antiquity to the Nineteenth Century
(Berlin [etc.]: Springer, 2010 [= Archimedes: New Studies in the History of Science and Technology, nr. 23]), pp. 151-202.
Studies on the Calendars and Eras used in the Almagest
- Ideler, Christian Ludwig, Historische Untersuchungen über die astronomischen Beobachtungen der Alten
(Berlin: C. Quien, 1806).
- Halma, Nicholas B., Table chronologique des règnes, prolongée jusqu’a la prise de Constantinople par les
Turcs; apparitions des fixes, de C. Ptolémée, Théon, etc., et introduction de Géminus aux phénomènes célestes [...],
suivies des recherches historiques sur les observations astronomiques des anciens, traduites de l’allemand de
M. Ideler, membre de l’Académie Royale de Prusse; et précédées d’un discours préliminaire et de deux
dissertations sur la réduction des années et des mois des anciens, a la forme actuelle des nôtres, pour servir à
l’intelligence de son édition grecque et française de l’Almageste (Paris: A. Bobée, 1819)
[Gallica link].
- Ideler, Christian Ludwig, Handbuch der mathematischen und technischen Chronologie (Berlin: August Rücker,
1825/26), 2 vols.
- Böckh, August, Zur Geschichte der Mondcyclen der Hellenen (Leipzig: B.G. Teubner, 1855 [= Jahrbüchern
für classische Philologie, Supplementband, N.F., Band I, Heft 1])
[Internet Archive link].
- Mommsen, Theodor, Die römische Chronologie bis auf Caesar (Berlin: Weidmannsche Buchhandlung, 1858)
[Internet Archive link].
- Lepsius, Richard, “Über einige Berührungspunkte der Aegyptischen, Griechischen und Römischen Chronologie”,
Monatsberichte der Königlichen Preußischen Akademie der Wissenschaften zu Berlin aus dem Jahre 1858 (Berlin:
Druckerei der Königl. Akademie der Wissenschaften, 1859), pp. 450-453
[Akademiebibliothek link].
- Böckh, August, “Eine Bemerkung über den zodiakalen Kalender des Astronomen Dionysios”, Monatsberichte der Königlichen
Preußischen Akademie der Wissenschaften zu Berlin aus dem Jahre 1858 (Berlin: Druckerei der Königl. Akademie der Wissenschaften,
1859), pp. 578-585
[Akademiebibliothek link] – reprinted in: E. Bratuscheck & P. Eichholtz (eds.), August
Boeckh’s akademische Abhandlungen vorgetragen in den Jahren 1836-1858 in der Akademie der Wissenschaften zu Berlin, nebst
einem Anhange epigraphische Abhandlungen aus Zeitschriften enthaltend (Leipzig: B.G. Teubner, 1872 [= August
Boeckh’s gesammelte kleine Schriften, Band VI]), pp. 374-381 [Google books link] ‒ see also the discussion in Monatsberichte der Königlichen Preußischen Akademie
der Wissenschaften zu Berlin aus dem Jahre 1859 (Berlin: Druckerei der Königl. Akademie der Wissenschaften, 1860), pp. 182-186
[Akademiebibliothek link].
- Böckh, August, Ueber die vierjährigen Sonnenkreise der Alten, vorzüglich den Eudoxischen: Ein Beitrag zur Geschichte
der Zeitrechnung und des Kalenderwesens der Aegypter, Griechen und Römer (Berlin: Georg Reimer, 1863)
[Internet Archive link].
- Meyer, Eduard, “Die chaldäische Aera des Almagest und der babylonische
Kalender”, Zeitschrift für Assyriologie und verwandte Gebiete, 9
(1894), 325-328 [Halle
link].
- Fotheringham, John Knight, “The Metonic and Callippic Cycles”, Monthly Notices of the Royal Astronomical Society, 84
(1924), 383-392 [ADS link].
- Kubitschek, Wilhelm, Grundriß der antiken Zeitrechnung (Munich: C.H. Beck’sche Verlagsbuchhandlung, 1928 [= Handbuch
der Altertumswissenschaft, Erste Abteiling, nr. VII]).
- Snyder, Walter F., “When was the Alexandrian Calendar Established?”, The American Journal of Philology,
64 (1943), 385-398 [JSTOR link].
- van der Waerden, Bartel Leendert, “Tables for the Egyptian and Alexandrian Calendar”, Isis,
47 (1956), 387-390 [JSTOR link].
- Neugebauer, Otto E., The Exact Sciences in Antiquity (Providence: Brown University Press, 1957), 2nd ed.
- van der Waerden, Bartel Leendert, “Greek Astronomical Calendars and their Relation to the Athenian Civil Calendar”, The Journal
of Hellenic Studies, 80 (1960), 168-180 [JSTOR link].
- Samuel, Alan E., Greek and Roman Chronology: Calendars and Years in Classical Antiquity (Munich: C.H. Beck’sche
Verlagsbuchhandlung, 1972 [= Handbuch der Altertumswissenschaft, Erste Abteiling, nr. VII]).
- van der Waerden, Bartel Leendert, “Greek Astronomical Calendars: I. The Parapegma of Euctemon”, Archive for History of Exact
Sciences, 29 (1984), 101-114 [SpringerLink].
- van der Waerden, Bartel Leendert, “Greek Astronomical Calendars: II. Callippos and his Calendar”, Archive for History of Exact
Sciences, 29 (1984), 115-124 [SpringerLink].
- van der Waerden, Bartel Leendert, “Greek Astronomical Calendars: III. The Calendar of Dionysios”, Archive for History of Exact
Sciences, 29 (1984), 125-130 [SpringerLink].
- van der Waerden, Bartel Leendert, “Greek Astronomical Calendars: IV. The Parapegma of the Egyptians and their “Perpetual Tables” ”,
Archive for History of Exact Sciences, 32 (1985), 95-104
[SpringerLink].
- van der Waerden, Bartel Leendert, “Greek Astronomical Calendars: V. The Motion of the Sun in the Parapegma of Geminos and in the
Romaka Siddhanta”, Archive for History of Exact Sciences, 34 (1985), 231-239
[SpringerLink].
- Goldstein, Bernard R. & Bowen, Alan C., “On Early Hellenistic Astronomy: Timocharis and the First Callippic Calendar”, Centaurus:
International Magazine of the History of Science and Medicine, 32 (1989), 272-293
[Wiley link].
- Skeat, Theodore Cressy, The Reign of Augustus in Egypt: Conversion
Tables for the Egyptian and Julian Calendars, 30 B.C. – 14 A.D. (Munich: C.H. Beck, 1993 [= Münchener Beiträge
zur Papyrusforschung und Antiken Rechtsgeschichte, nr. 84]).
- Hagedorn, Dieter, “Zum ägyptischen Kalender unter Augustus”, Zeitschrift für Papyrologie und Epigraphik, 100 (1994),
211-222 [JSTOR link].
- Hagedorn, Dieter & Worp, Klaas A., “Das Wandeljahr im römischen Ägypten”, Zeitschrift für Papyrologie und Epigraphik,
104 (1994), 243-255 [JSTOR link].
- Jones, Alexander R., Astronomical Papyri from Oxyrhynchus (Philadelphia: American Philosophical Society, 1999 [=
Memoirs of the American Philosophical Society, nr. 233]), 2 vols.
- Jones, Alexander R., “Calendrica I: New Callippic Dates”, Zeitschrift für Papyrologie und Epigraphik, 129 (2000),
141-158 [JSTOR link].
- Jones, Alexander R., “Calendrica II: Date Equations from the Reign of Augustus”, Zeitschrift für Papyrologie und Epigraphik,
129 (2000), 159-166 [JSTOR link].
- Skeat, Theodore Cressy, “A Forgotten Factor in the Debate on the Calendar in Augustan Egypt”, Zeitschrift für Papyrologie und
Epigraphik, 132 (2000), 240 [JSTOR link].
- Skeat, Theodore Cressy, “The Egyptian Calendar under Augustus”, Zeitschrift für Papyrologie und Epigraphik,
135 (2001), 153-156 [JSTOR link].
- Jones, Alexander R., “A Posy of Almagest Scholia”, Centaurus: International Magazine of the History of Science and
Medicine, 45 (2003), 69-78 [Wiley
link].
- Bennett, Chris, “The Early Augustan Calendars in Rome and Egypt”, Zeitschrift für Papyrologie und Epigraphik, 142 (2003),
221-240 [JSTOR link].
- Bennett, Chris, “The Early Augustan Calendars in Rome and Egypt: Addenda et Corrigenda”, Zeitschrift für Papyrologie und Epigraphik,
147 (2004), 165-168 [JSTOR link].
- Krauss, Rolf, “August Böckh (1785-1867) und andere Authoren über den Beginn des ägyptischen Kalendertages nach Ptolemäus im Almagest”,
Studien zur Altägyptischen Kultur, 32 (2004), 275-286 [JSTOR
link].
- Evans, James & Berggren, J. Lennart, Geminos’s Introduction to the Phenomena: A Translation and Study of a Hellenistic Survey
of Astronomy (Princeton/Oxford: Princeton University Press, 2006), pp. 89-92.
- Jones, Alexander R., “On Greek Stellar and Zodiacal Date-Reckoning”, in: J.M. Steele (ed.), Calendars and Years: Astronomy and
Time in the Ancient Near East (Oxford: Oxbow Books, 2007), pp. 149-167.
On the Supposed Discovery of the Third Lunar Inequality ("Variation") by Islamic Astronomers [not yet
checked/incomplete links]
- Sédillot, Louis-Pierre-Eugène Amélie, “Recherches nouvelles pour servir à l'histoire de l'astronomie chez les Arabes: Découverte
de la variation, par Aboul-Wefâ, astronome du Xe siècle”, Nouveau journal asiatique, ou recueil de mémoires, d'extraits et de notices
relatifs à l'histoire, à la philosophie, aux langues et à la littérature des peuples orientaux, série 2, 16 (1835), 420-438
[Gallica link].
- Sédillot, Louis-Pierre-Eugène Amélie, “Sur un manuscrit arabe dans lequel se trouve signalée l'inégalité du mouvement de la lune
connue des astronomes sous le nom de variation”, Comptes rendus hebdomadaires des séances de l'Académie des sciences, 2
(1836), 202-205 [Gallica link].
- Sédillot, Louis-Pierre-Eugène Amélie, “Note sur la découverte de la variation, par Aboul-Wefâ, astronome du 10e siècle”, Comptes
rendus hebdomadaires des séances de l'Académie des sciences, 2 (1836), 258-261
[Gallica link] – with a sceptical note from
Guillaume Libri, 261-264 [Gallica link].
- Sédillot, Louis-Pierre Eugène Amélie, “Réponse aux nouvelles objections présentées sur la découverte de la variation par Aboul Wefâ,
astronome du 10e siècle”, Comptes rendus hebdomadaires des séances de l'Académie des sciences, 2 (1836), 301-307
[Gallica link].
- Arago, François & Mathieu, Claude-Louis, “Rapport sur un mémoire de M. Am. Sédillot, sur les instruments astronomiques des Arabes”,
Comptes rendus hebdomadaires des séances de l'Académie des sciences, 7 (1838), 1015-1017
[Gallica link].
- Munk, Salomon, “Sur les découvertes attribuées aux Arabes, relativement aux inégalitiés dans le mouvement de la lune”, Comptes rendus
hebdomadaires des séances de l'Académie des sciences, 16 (1843), 1444-1446
[Gallica link] – with a reply by Sédillot, 1446-1448
[Gallica link].
- Munk, Salomon, “Nouvelle note concernant la part qu'ont eue les Arabes à la découverte des inégalitiés du mouvement de la lune”,
Comptes rendus hebdomadaires des séances de l'Académie des sciences, 17 (1843), 76-80
[Gallica link].
- Sédillot, Louis-Pierre Eugène Amélie, “Sur la détermination de la troisième inégalité lunaire ou variation par les Arabes”, Comptes
rendus hebdomadaires des séances de l'Académie des sciences, 17 (1843), 163-173
[Gallica link].
- Biot, Jean-Baptiste, “Sur la découverte de l'inégalité lunaire appelée la variation”, Comptes rendus hebdomadaires des séances de
l'Académie des sciences, 17 (1843), 1315-1316 [Gallica link].
- Biot, Jean-Baptiste, "Sur un traité arabe relatif à l'astronomie", Journal des Savants pour l'année 1843, 513-532[?]
[Gallica link], 609-626
[Gallica link], 694-703
[Gallica link] & 719-737
[Gallica link].
- Sédillot, Louis-Pierre Eugène Amélie, “Sur la découverte de la variation”, Comptes rendus hebdomadaires des séances de l'Académie
des sciences, 18 (1844), 48 [Gallica link].
- Biot, Jean-Baptiste, “Remarques sur la lettre précédente”, Comptes rendus hebdomadaires des séances de l'Académie des sciences,
18 (1844), 49 [Gallica link].
- Sédillot, Louis-Pierre Eugène Amélie, “De la latitude de la lune”, Comptes rendus hebdomadaires des séances de l'Académie des
sciences, 19 (1844), 1027-1029 [Gallica link].
- Sédillot, Louis-Pierre Eugène Amélie, “Réponse à quelques observations nouvelles sur la découverte de la variation, ou troisième inégalité
lunaire, par les astronomes arabes du Xe siècle”, Comptes rendus hebdomadaires des séances de l'Académie des sciences, 20
(1845), 1308-1309 [Gallica link] – with a reply by
Biot, 1309 [Gallica link].
- Biot, Jean-Baptiste, “Sur un exposé de la théorie de la lune, rédigé par un auteur arabe du Xe siècle”, Journal des Savants pour
l'année 1845, 149-166 [Gallica link].
- Sédillot, Louis-Pierre-Eugène Amélie, Matériaux pour servir à l'histoire comparée des sciences mathématiques chez les Grecs et
les Orientaux (Paris: ???, 1845/49), 2 vols. [Internet Archive link / Internet Archive link].
- Michal, ?., “Note sur une inégalité de la lune, signalée par Aboulwefa, astronome arabe de Bagdad, qui vivait au Xe siècle”, Comptes
rendus hebdomadaires des séances de l'Académie des sciences, 30 (1850), 629-633
[Gallica link].
- Biot, Jean-Baptiste, “Remarques sur une note de M. MIchal, relative à la découverte de la variation”, Comptes rendus hebdomadaires
des séances de l'Académie des sciences, 30 (1850), 637-638 [Gallica link].
- Chasles, Michel, “Lettre à M. Am.-L. Sédillot sur la découverte de la variation lunaire par Aboul Wéfa”, Comptes rendus
hebdomadaires des séances de l'Académie des sciences, 54 (1862), 1002-1012
[Gallica link].
- Sédillot, Louis-Pierre Eugène Amélie, “De la détermination de la troisième inégalité lunaire ou variation, par Aboul-Wéfâ et Tycho-Brahé”,
Comptes rendus hebdomadaires des séances de l'Académie des sciences, 66 (1868), 286-289
[Gallica link].
- Bertrand, Joseph-François, “Note sur la théorie de la lune d'Aboul Wefâ”, Comptes rendus hebdomadaires des séances de l'Académie
des sciences, 73 (1871), 581-589 [Gallica link].
- Chasles, Michel, “Sur la découverte de la variation lunaire”, Comptes rendus hebdomadaires des séances de l'Académie des sciences,
73 (1871), 637-647 [Gallica link].
- Bertrand, Joseph-François, “Observations sur la note de M. Chasles, relative à la découverte de la variation lunaire”, Comptes
rendus hebdomadaires des séances de l'Académie des sciences, 73 (1871), 765-766
[Gallica link].
- Chasles, Michel, “Réponse à un passage de la note de M. Bertrand insérée dans le Compte rendu de la dernière séance”, Comptes
rendus hebdomadaires des séances de l'Académie des sciences, 73 (1871), 805-808
[Gallica link].
- Bertrand, Joseph-François, “Réponse à la note de M. Chasles”, Comptes rendus hebdomadaires des séances de l'Académie des
sciences, 73 (1871), 889 [Gallica link] – with
comments by Leverrier and Chasles, 890 [Gallica link].
- Chasles, Michel, “Réponse aux observations présentées dans la dernière séance par M. Bertrand, à propos d'Aboul-Wefâ”, Comptes
rendus hebdomadaires des séances de l'Académie des sciences, 73 (1871), 932-934
[Gallica link].
- Sédillot, Louis-Pierre Eugène Amélie, “Des savants arabes et des savants d'aujourd'hui, à propos de quelques rectifications”,
Bullettino di bibliografia e di storia delle scienze matematiche e fisiche, 4 (1871), 401-418
[Internet Archive link].
- Bertrand, Joseph-François, “La théorie de la lune d'Aboul Wefâ”, Journal des Savants pour l'année 1871, 457-474 [Gallica
link].
- Chasles, Michel, “Sur la découverte de la variation par Aboul-Wefâ”, Comptes rendus hebdomadaires des séances de l'Académie des
sciences, 76 (1873), 859-864 [Gallica link].
- Chasles, Michel, “Explication du texte d'Aboul-Wefâ sur la troisième inégalité de la lune”, Comptes rendus hebdomadaires des
séances de l'Académie des sciences, 76 (1873), 901-909 [Gallica link] – with a concluding note by Bertrand, 909-911
[Gallica link].
- Sédillot, Louis-Pierre Eugène Amélie, “Rectification d'un point de la communication de M. Munk, au sujet de la découverte de
la variation”, Comptes rendus hebdomadaires des séances de l'Académie des sciences, 76 (1873), 1291-1293
[Gallica link].
- Sédillot, Louis-Pierre Eugène Amélie, “Sur les emprunts que nous avons fait à la science arabe, et en particulier de la détermination de
la troisième inégalité lunaire ou variation par Aboul-Wefā de Bagdad”, Bullettino di bibliografia e di storia delle scienze matematiche
e fisiche, 8 (1875), 63-78 [Internet Archive link].
- Sédillot, Louis-Pierre Eugène Amélie, Histoire générale des Arabes: Leur empire, leur civilisation, leurs écoles philosphiques,
scientifiques et littéraires. Deuxième édition (Paris: Maisonneuve et Cie, 1877), 2 vols. [Internet Archive link / Internet Archive
link] – cited as HGA.
- Anschütz, Carl, “Ueber die Entdeckung der Variation und der jährlichen Gleichung des Mondes”, Zeitschrift für Mathematik und Physik:
Historisch-Literarisch Abtheilung, 31 (1886), 161-171 [GDZ link], 202-219 [GDZ link]; 32 (1887), 1-15 [GDZ link].
- Carra de Vaux, Camille Marie Bernard, “L'almageste d'Abû'lwéfa Albûzdjâni”, Journal asiatique, ou recueil de mémoires,
d'extraits et de notices relatifs à l'histoire, à la philosophie, aux langues et à la littérature des peuples orientaux,
série 8, 19 (1892), 408-471 [Gallica link].
- Herz, Norbert, “Zur vermeintlichen Entdeckung der »Variation« durch Abul-Wefâ”, Astronomische Nachrichten, 129 (1892),
351-354 [ADS link].
- Nau, François, “La troisième inégalité lunaire dans Aboulfaradj (Bar Hebreus)”, Bulletin astronomique, série I, 10 (1893),
259-264 [ADS link].
- Thoren, Victor E., “Tycho and Kepler on the Lunar Theory”, Publications of the Astronomical Society of the Pacific, 79 (1967),
482-489 [ADS link].
- Charette, François, Orientalisme et histoire des sciences: L'historiographie européenne des sciences islamiques et hindoues,
1784-1900 (Montreal: Département d'Histoire de l'Université de Montréal, 1995), chapter 5 & annexe D.
Online Resources
I am grateful to Dennis Duke and Yaaqov Loewinger for suggesting corrections and improvements.
Return to the main page
last updated on 27 October 2016
