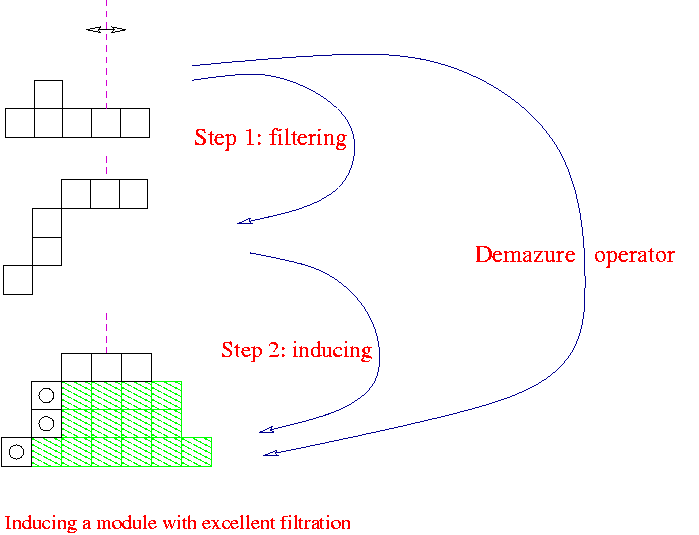
We think of the top diagram in the picture as giving dimensions of eigenspaces for a certain diagonalized group element t in a given representation. In this example t has eigenvalues say x-3, x-2, x-1, 1, x, with respective multiplicities 1, 2 (two boxes in same column), 1, 1, 1. One says that t has formal character x-3+2x-2+ x-1+ 1+ x. The dashed "reflection hyperplane" goes through the box which belongs to the eigenvalue 1. The Demazure operator produces the multiplicities of eigenvalues for the action of t in the "induced representation". Its diagram has a symmetry with respect to the reflection hyperplane.
In the example the new multiplicities are 1, 3, 4, 4, 4, 3, 1 for eigenvalues x-3 through x3 respectively. This is depicted in the bottom diagram. More details on the procedure are given below. The example is taken from the class of representations "with excellent filtration", as discussed in our book "Lectures on Frobenius Splittings and B-modules"(PDF). For this class the Demazure operators are simplest. No virtual representations (negative multiplicities) intervene. Thus, in the picture there are no boxes to be subtracted, only boxes to be added.
The picture attempts to tell us that the formal character x-3+2x-2+ x-1+ 1+ x should first be written as a sum of terms that are either of the form x-j with j nonnegative or of the form of a "ladder sum" x-j+...+xj, again with j nonnegative. There are four terms, corresponding with the four rows in the middle diagram. In formulas: x-3+2x-2+ x-1+ 1+ x is written as the ladder sum x-1+ 1+ x, plus x-2, plus x-2, plus x-3.
Next one should leave the ladder sums as they are and complete a term of the form x-j to the corresponding ladder sum x-j+...+xj. In the bottom diagram the white boxes in a row encode the earlier term and the full row encodes the ladder sum. The terms that are not ladder sums to begin with have been marked with circles.
Of course such decomposition into terms only works for formal characters of a special type, such as formal characters of representations with excellent filtration. If the midddle diagram symbolizes a natural excellent filtration, then the top row in this diagram corresponds with the character of the bottom layer in the excellent filtration, the second row with the character of the next layer and so on. So in a sense this middle diagram is upside down and the bottom diagram as well.
We start with
. . .
. . . .
. . . . .
. . . .
1 . .
So we start with a one dimensional representation positioned at the
lowest weight.
Applying the Demazure operator "going east", the character becomes
. . .
. . . .
. . . . .
. . . .
1 1 1
then applying the Demazure operator "going northwest" (in parallel, once for each
northwest oriented strip), the character becomes
1 . .
1 1 . .
1 1 1 . .
1 1 1 .
1 1 1
then applying the Demazure operator going east again we get
1 1 1
1 2 2 1
1 2 3 2 1
1 2 2 1
1 1 1
We have now reached the highest weight and the result gives
the Weyl character that we sought. It is
stable under both types of Demazure operators. The dimension of the representation is 27,
the sum of the multiplicities. This method of computing without signs (no negative terms) uses the fact that the class of modules with excellent filtration is closed under the relevant inductions and restrictions. See lemma 3.2.11 and theorem 6.3.1 in our book. Without this, one would need the full form of the Demazure operator, sending xj to (xj-x-j+1)/(1-x). Nowadays there are several models to justify the sign free computation method.