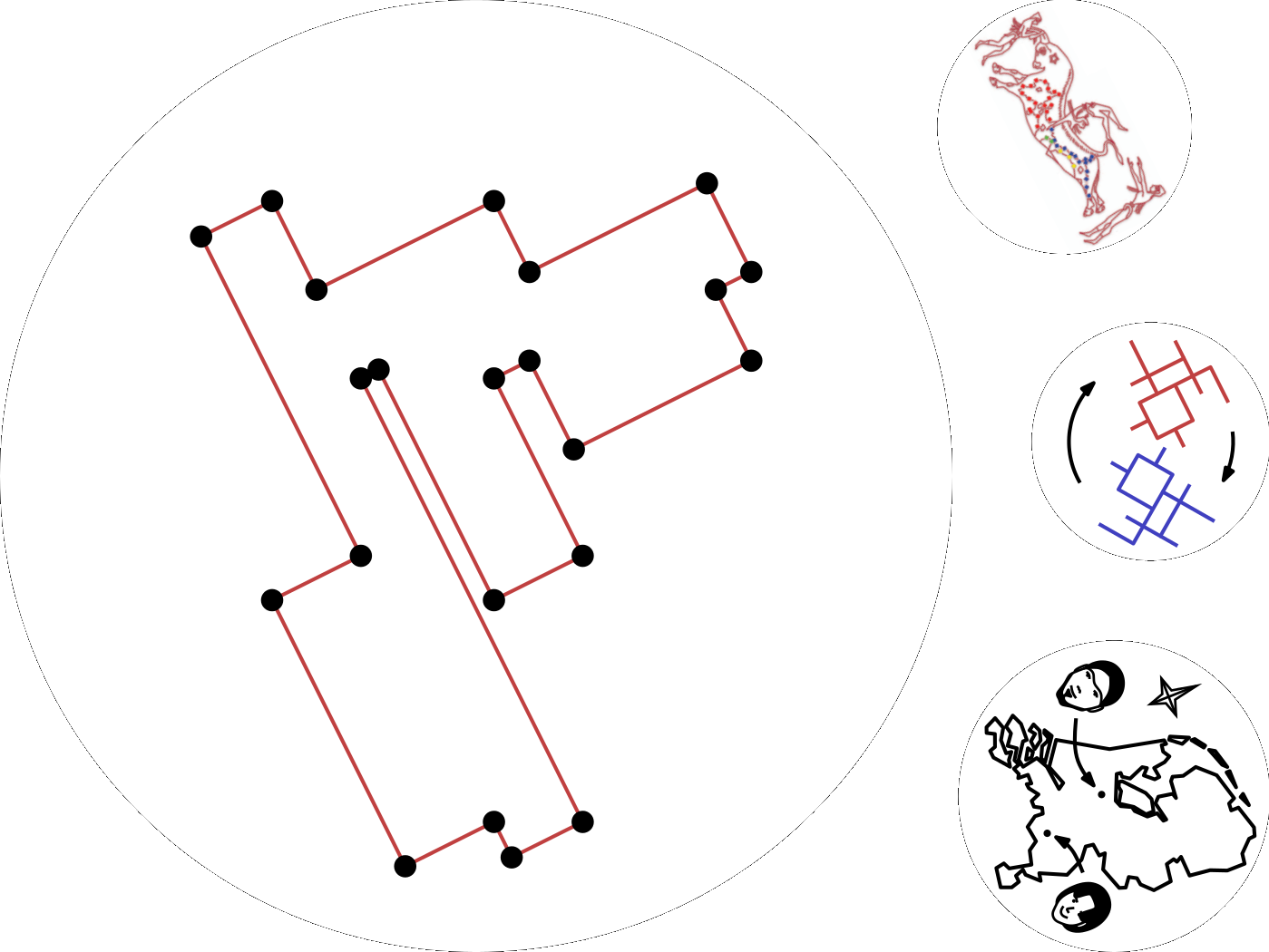
Connected Rectilinear Graphs on Point Sets

Let V be a set of n points in R^d. We study the question whether there exists an orientation such that V is the vertex set of a connected rectilinear graph in that orientation. A graph is rectilinear if its edges are straight line segments in d pairwise perpendicular directions. We prove that at most one such orientation can be possible, up to trivial rotations of 90 degrees around some axis. In addition, we present an algorithm for computing this orientation (if it exists) in O(n^d) time when d is at least 2.

slides

Journal Article (peer-reviewed)

Conference Proceedings (peer-reviewed)

Workshop or Poster (weakly reviewed)

Technical Report (not reviewed)

back to list