Largest and Smallest Convex Hulls for Imprecise Points

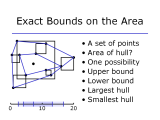
Assume that a set of imprecise points is given, where each point is specified by a region in which the point may lie. We study the problem of computing the smallest and largest possible convex hulls, measured by length and by area. Generally we assume the imprecision region to be a square, but we discuss the case where it is a segment or circle as well. We give polynomial time algorithms for several variants of this problem, ranging in running time from O(nlogn) to O(n¹³), and prove NP-hardness for some other variants.

slides

Journal Article (peer-reviewed)

Conference Proceedings (peer-reviewed)

Workshop or Poster (weakly reviewed)

Technical Report (not reviewed)

back to list