Quantum simulations with ultracold atoms in optical lattices 

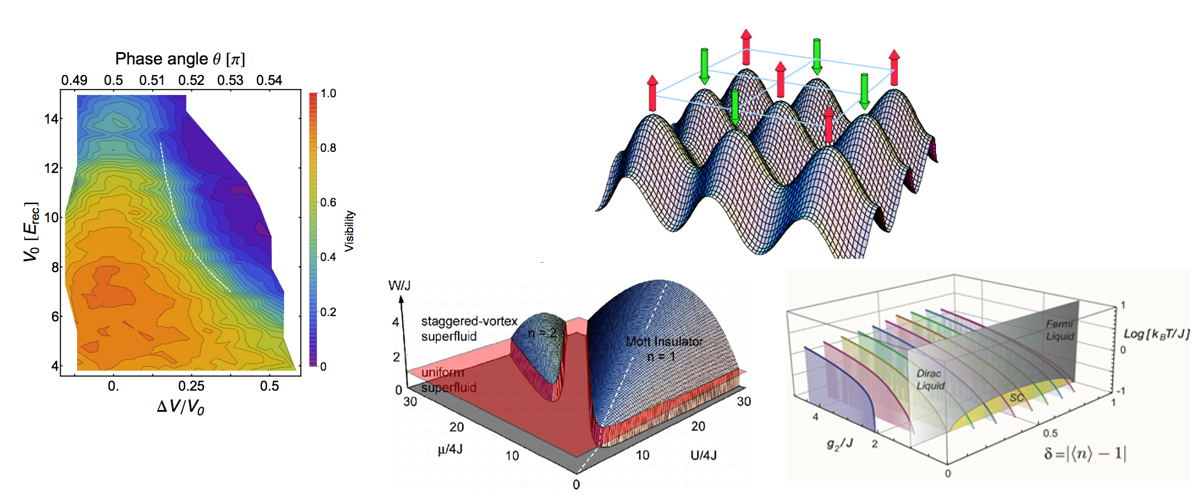
Feynman’s original idea of using one quantum system that can be controlled to simulate the behavior of another more complex one has flourished during the last decades in the field of cold atoms. Ultracold atoms in optical lattices are ideal quantum simulators because several parameters can be manipulated at will: the geometry of the lattice can be made square, triangular, honeycomb, Lieb, or bipartite; the hopping parameter can be tuned upon varying the lattice potential amplitude, interactions can be made attractive, repulsive, or absent by using Feshbach resonances, disorder is absent, but can be artificially introduced if desired, a gauge field can be synthetically applied, and the lattice can be loaded with fermions, bosons, or a mixture of both. One important recurrent question is whether cold atoms will help us to understand high-Tc superconductors. We have recently elucidated the topological character of the Varma phase, which is one of the proposals for describing the pseudogap regime of high-Tc cuprates [1]. Structural phase transitions are known to play an important role for superconductivity. To clarify this issue, we considered a bipartite optical lattice and unveiled the loss of phase coherence upon structural changes of the lattice. The experiments exhibited an excellent agreement with our theory (white dashed line in the figure, separating the Mott insulating (blue) and superfluid (yellow) phases [2]. We have also proposed a setup to experimentally realize the so-called eta-pairing superconductor first proposed by Yang in 1988. By shaking the Feshbach resonance, we show how a correlated-hopping model hosting a phase with eta pairs emerges in the high-frequency regime [3]. Another interesting open question in the physics of high-Tc cuprates is whether and how the time-reversal-symmetry (TRS) broken pseudogap phase influences superconductivity. We have shown that it is possible to generate a staggered gauge field in a square lattice using a bichromatic light field [4]. This setup allows one to reach a TRS broken phase that hosts a staggered vortex superfluid [5]. By loading this system with a Fermi-Bose mixture, we found that a long-range interaction between fermions may arise, mediated by the phonons of the BEC. This system displays all the main features known to occur in the high-Tc cuprate phase diagram (see figure) [6]. 

[1] Topological Varma superfluid in optical lattices

M. Di Liberto, A. Hemmerich, C. Morais Smith, 

Pays. Rev. Lett., 117, 163001 (2016).

[2] Controlling coherence via tuning of the population imbalance in a bipartite optical lattice, 

M. Di Liberto, T. Comparin, T. Kock, M. Ölschläger, A. Hemmerich, C. Morais Smith, 

Nature Commun. 5, 5735 (2014).

[3] Quantum simulation of correlated-hopping models with fermions in optical lattices,

M. Di Liberto, C. E. Creffield, G. I. Japaridze, C. Morais Smith,

Phys. Rev. A 89, 013624 (2014).

[4] Exciting a d-density wave in an optical lattice with driven tunneling,

A. Hemmerich and C. Morais Smith,

Phys. Rev. Lett. 99, 113002 (2007). 

Editor’s choice of Science magazine: scientifical highlights in physics (Sep. 28 2007).

[5] Staggered-vortex superfluid of ultracold bosons in an optical lattice,

Lih-King Lim, C. Morais Smith and A. Hemmerich, 

Phys. Rev. Lett. 100, 130402 (2008).

[6] Competing pairing states for ultracold fermions in optical lattices with an artificial staggered magnetic field,

Lih-King Lim, A. Lazarides, A. Hemmerich, and C. Morais Smith,

Phys. Rev. A 82, 013616 (2010).