Quantum Electrodynamics of low-dimensional systems

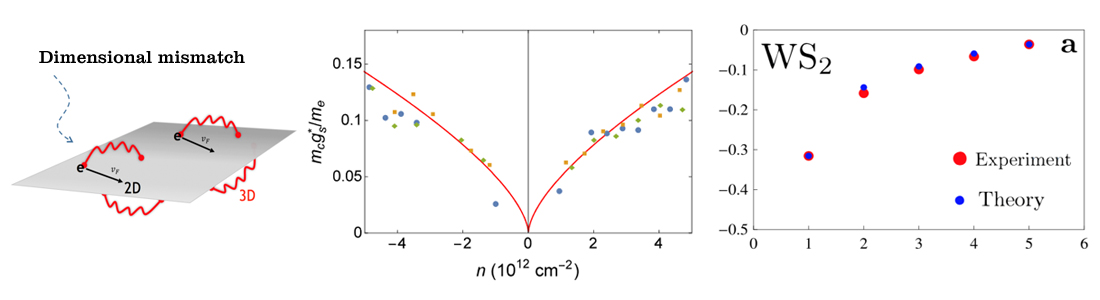
We use Pseudo Quantum Electrodynamics (PQED) in order to describe the full electromagnetic interaction of electrons in graphene [1,2] or transition-metal-dichalcogenides [3] in a consistent 2D formulation (see figure). The theory is dual to Maxwell QED in 2+1 dimensions [4]. We first consider the effect of this interaction in the vacuum polarization tensor or, equivalently, in the current correlator. This allows us to obtain the dc conductivity in Kubo's formula. We predict the onset of an interaction-driven spontaneous Quantum Valley Hall effect (QVHE) in graphene below a critical temperature of the order of 0.05 K [1]. Then, we calculate the corrections to the g-factor of graphene due to interactions. The theoretical results show an excellent agreement with experiments [2]. In the case of transition-metal-dichalcogenides, we calculate the exciton energies using the Bethe-Salpeter and Schwinger-Dyson equations. Our results show an excellent agreement with experiments, without fitting parameters (see figure). Moreover, we show how the dynamical PQED interaction reduces to the Keldysh potential in the static limit [3]. The formalism was also developed upon projection from (3+1)D into (1+1)D, thus leading to a Conformal QED (CQED) [4]. It has been shown recently that local four-fermion interactions on the edges of 2D time-reversal-invariant topological insulators give rise to a new non-Fermi-liquid phase, called helical Luttinger liquid (HLL). We provided a first-principle derivation of this non-Fermi-liquid phase based on the gauge-theory approach. By integrating out the gauge field in the corresponding partition function, we showed that the CQED gives rise to a 1+1-dimensional Thirring model. The bosonized Thirring Hamiltonian describes exactly a HLL with a parameter K and a renormalized Fermi velocity that depend on the value of the fine-structure constant α.

[1] Interaction Induced Quantum Valley Hall Effect in Graphene,

E. C. Marino, Leandro O. Nascimento, V. S. Alves, and C. Morais Smith, 

Phys. Rev. X 5, 011040 (2015).

[2] Spin g-factor due to electronic interactions in graphene,

N. Menezes, V. S. Alves, E. C. Marino, L. Nascimento, L. O. Nascimento, and C. Morais Smith, 

Phys. Rev. B 95, 245138 (2017).

[3] Quantum-electrodynamical approach to the exciton spectrum in Transition-Metal Dichalcogenides,

E. C. Marino, Leandro O. Nascimento, V. S. Alves, N. Menezes, and C. Morais Smith, 

2D Materials 5, 041006 (2018).

[4] Unitarity of theories containing fractional powers of the d'Alembertian operator,

E. C. Marino, Leandro O. Nascimento, V. S. Alves, and C. Morais Smith, 

Phys. Rev. D 90, 105003 (2014).

[5] Conformal QED in two-dimensional topological insulators,

N. Menezes, G. Palumbo, and C. Morais Smith, 

Nature Scientific Reports 7, 14175 (2017).