

Next: About this
Up: schema
Previous: Seminarium: Grootschalige
- 1
-
W. E. ARNOLDI, The principle of minimized iteration in the solution
of the matrix eigenvalue problem, Quart. Appl. Math., 9 (1951), pp. 17-29.
- 2
-
Z. BAI AND J. DEMMEL, Using the matrix sign function to compute
invariant subspaces, SIAM J. Matrix Anal. Appl., 19 (1998), pp. 205-225
(electronic).
- 3
-
Z. BAI, J. DEMMEL, J. DONGARRA, A. RUHE, AND H. VAN DER VORST, eds., Templates for the solution of algebraic eigenvalue problems, Society for
Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2000.
A practical guide.
- 4
-
Z. BAI, P. FELDMANN, AND R. W. FREUND, How to make theoretically
passive reduced-order models passive in practice, in Proceedings of the
IEEE 1998 Custom Integrated Circuits Conference, IEEE, 1998, pp. 207-210.
- 5
-
Z. BAI AND Q. YE, Error estimation of the Padé approximation of
transfer functions via the Lanczos process, Electron. Trans. Numer. Anal.,
7 (1998), pp. 1-17 (electronic).
Large scale eigenvalue problems (Argonne, IL, 1997).
- 6
-
R. BARRETT, M. BERRY, T. F. CHAN, J. DEMMEL, J. DONATO, J. DONGARRA,
V. EIJKHOUT, R. POZO, C. ROMINE, AND H. VAN DER VORST, Templates for
the Solution of Linear Systems: Building Blocks for Iterative Methods,
Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA,
1994.
- 7
-
A. BJÖRCK, Solving linear least squares problems by
Gram-Schmidt orthogonalisation, BIT, 7 (1967), pp. 1-21.
- 8
-
Å. BJÖRCK AND C. C. PAIGE, Loss and recapture of
orthogonality in the modified Gram-Schmidt algorithm, SIAM J. Matrix
Anal. Appl., 13 (1992), pp. 176-190.
- 9
-
W. BOMHOF, Jacobi-Davidson methods for eigenvalue problems in
pole zero analysis, Unclassified Report 012/97, National Laboratory, Philips
Electronics, Eindhoven, the Netherlands, July 1997.
- 10
-
J. DANIEL, W. GRAGG, L. KAUFMAN, AND G. STEWART, Reorthogonalization
and stable algorithms for updating the Gram-Schmidt QR factorization,
Math. Comp., 30 (1976), pp. 772-795.
- 11
-
R. FLETCHER, Conjugate gradient methods for indefinite systems, in
Numerical Analysis Dundee 1975, Lecture Notes in Mathematics 506, G. Watson,
ed., Berlin, Heidelberg, New York, 1976, Springer-Verlag, pp. 73-89.
- 12
-
D. R. FOKKEMA, G. L. G. SLEIJPEN, AND H. A. VAN DER VORST, Jacobi-Davidson style QR and QZ algorithms for the reduction of
matrix pencils, SIAM J. Sci. Comput., 20 (1999), pp. 94-125 (electronic).
- 13
-
R. W. FREUND, Reduced-order modeling techniques based on Krylov
subspaces and their use in circuit simulation, Tech. Report Numerical
Analysis Manuscript No. 98-3-02, Bell Laboratories, Murray Hill, New
Jersey, USA, 1998.
To appear in Applied and Computational Control, Signals, and
Circuits.
- 14
-
height 2pt depth -1.6pt width 23pt, Krylov-subspace
methods for reduced-order modeling in circuit simulation, Tech. Report
Numerical Analysis Manuscript No. 98-3-02, Bell Laboratories, Murray Hill,
New Jersey, USA, 1999.
To appear in ???
- 15
-
R. W. FREUND AND P. FELDMANN, Reduced-order modeling of large linear
passive multi-terminal circuits using matrix-Padé approximation, in
Proceedings of the Design, Automation and Test in Europe Conference 1998,
IEEE Computer Society Press, 1998, pp. 530-537.
- 16
-
R. W. FREUND AND N. M. NACHTIGAL, QMR: a quasi-minimal residual
method for non-Hermitian linear systems, Numer. Math., 60 (1991),
pp. 315-339.
- 17
-
L. GIRAUD AND L. J. LANGOU, Robust selective Gram-Schmidt
reorthogonalization, Technical Report TR/PA/02/52, CERFACS, Toulouse,
France, 2002.
Submitted to SISC Copper Mountain Special Issue.
- 18
-
height 2pt depth -1.6pt width 23pt, When modified
Gram-Schmidt generates a well-conditioned set of vectors, IMA
Journal of Numerical Analysis, 22 (2002), pp. 521-528.
- 19
-
L. GIRAUD, L. JUCIEN, AND R. MIRO, On the round-off error analysis
of the Gram-Schmidt algorithm with reorthogonalization, Technical Report
TR/PA/02/33, CERFACS, Toulouse, France, 2002.
- 20
-
A. GREENBAUM, M. ROZLOZNÍK, AND Z. STRAKOš, Numerical behaviour of the modified Gram-Schmidt GMRES
implementation, BIT, 37 (1997), pp. 706-719.
Direct methods, linear algebra in optimization, iterative methods
(Toulouse, 1995/1996).
- 21
-
E. J. GRIMME, D. C. SORENSEN, AND P. VAN DOOREN, Model reduction of
state space systems via an implicitly restarted Lanczos method, Numer.
Algorithms, 12 (1996), pp. 1-31.
- 22
-
W. HOFFMANN, Iterative algorithms for Gram-Schmidt
orthogonalization, Computing, 41 (1989), pp. 335-348.
- 23
-
C. LANCZOS, An iteration method for the solution of the eigenvalue
problem of linear differential and integral operators, J. Res. Nat. Bur.
Stand., 45 (1950), pp. 255-282.
- 24
-
R. B. MORGAN, Computing interior eigenvalues of large matrices,
Linear Algebra Appl., 154/156 (1991), pp. 289-309.
- 25
-
C. C. PAIGE, B. N. PARLETT, AND H. A. VAN DER VORST, Approximate
solutions and eigenvalue bounds from Krylov subspaces, Numer. Linear
Algebra Appl., 2 (1995), pp. 115-133.
- 26
-
B. N. PARLETT, The Symmetric Eigenvalue Problem, Prentice-Hall
Series in Computational Mathematics, Prentice-Hall, Englewood Cliffs, N.J.,
1980.
- 27
-
A. RUHE, Numerical aspects of Gram-Schmidt orthogonalization of
vectors, Linear Algebra Appl., 52/53 (1983), pp. 591-601.
- 28
-
Y. SAAD, Numerical Methods for Large Eigenvalue Problems,
Manchester University Press, Manchester, UK, 1992.
- 29
-
G. L. G. SLEIJPEN, Gram-Schmidt orthogonalisation.
Personel notes, Januari 2000.
- 30
-
G. L. G. SLEIJPEN AND H. A. VAN DER VORST, A Jacobi-Davidson
iteration method for linear eigenvalue problems, SIAM J. Matrix Anal. Appl.,
17 (1996), pp. 401-425.
- 31
-
P. SONNEVELD, CGS, a fast Lanczos-type solver for nonsymmetric
linear systems, SIAM J. Sci. Statist. Comput., 10 (1989), pp. 36-52.
- 32
-
J. VAN DEN ESHOF, Analysis of nested iteration methods for
nonlinear problems, Ph.D. thesis, Utrecht University, Utrecht, The
Netherlands, September 2003.
- 33
-
H. A. VAN DER VORST, An iterative solution method for solving
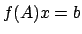 , using Krylov subspace information obtained for the symmetric
positive definite matrix
, using Krylov subspace information obtained for the symmetric
positive definite matrix 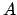 , J. Comput. Appl. Math., 18 (1987),
pp. 249-263.
, J. Comput. Appl. Math., 18 (1987),
pp. 249-263.
- 34
-
H. A. VAN DER VORST, Bi-CGSTAB: A fast and smoothly converging variant of
Bi-CG for the solution of nonsymmetric linear systems, SIAM J. Sci.
Stat. Comput., 13 (1992), pp. 631-644.
- 35
-
H. A. VAN DER VORST, Iterative methods
for large linear systems.
Lecture notes on iterative methods, June 2002.
- 36
-
H. A. VAN DER VORST, Computational
Methods for Large Eigenvalue Problems, Elsevier, North Holland, 2003.
To be published.

Gerard L.G. Sleijpen
2003-02-17