Bibliography

1

Z. BAI AND J. DEMMEL, Using the matrix sign function to compute invariant subspaces, SIAM J. Matrix Anal. Appl., 19 (1998), pp. 205-225 (electronic).

2

R. BARRETT, M. BERRY, T. F. CHAN, J. DEMMEL, J. DONATO, J. DONGARRA, V. EIJKHOUT, R. POZO, C. ROMINE, AND H. VAN DER VORST, Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1994.

3

M. BENZI, Preconditioning techniques for large linear systems: a survey, J. Comput. Phys., 182 (2002), pp. 418-477.

4

M. BENZI AND M. T0=0=0 0 BY1PTTO00 #MATH16#U"UMA, A sparse approximate inverse preconditioner for nonsymmetric linear systems, SIAM J. Sci. Comput., 19 (1998), pp. 968-994 (electronic).

5

height 2pt depth -1.6pt width 23pt, Orderings for factorized sparse approximate inverse preconditioners, SIAM J. Sci. Comput., 21 (2000), pp. 1851-1868 (electronic).
Iterative methods for solving systems of algebraic equations (Copper Mountain, CO, 1998).

6

height 2pt depth -1.6pt width 23pt, A robust incomplete factorization preconditioner for positive definite matrices, Numer. Linear Algebra Appl., 10 (2003), pp. 385-400.
Preconditioning, 2001 (Tahoe City, CA).

7

A. BJÖRCK, Solving linear least squares problems by Gram-Schmidt orthogonalisation, BIT, 7 (1967), pp. 1-21.

8

Å. BJÖRCK AND C. C. PAIGE, Loss and recapture of orthogonality in the modified Gram-Schmidt algorithm, SIAM J. Matrix Anal. Appl., 13 (1992), pp. 176-190.

9

J. DANIEL, W. GRAGG, L. KAUFMAN, AND G. STEWART, Reorthogonalization and stable algorithms for updating the Gram-Schmidt QR factorization, Math. Comp., 30 (1976), pp. 772-795.

10

R. FLETCHER, Conjugate gradient methods for indefinite systems, in Numerical Analysis Dundee 1975, Lecture Notes in Mathematics 506, G. Watson, ed., Berlin, Heidelberg, New York, 1976, Springer-Verlag, pp. 73-89.

11

R. W. FREUND AND N. M. NACHTIGAL, QMR: a quasi-minimal residual method for non-Hermitian linear systems, Numer. Math., 60 (1991), pp. 315-339.

12

L. GIRAUD AND L. J. LANGOU, Robust selective Gram-Schmidt reorthogonalization, Technical Report TR/PA/02/52, CERFACS, Toulouse, France, 2002.
Submitted to SISC Copper Mountain Special Issue.

13

height 2pt depth -1.6pt width 23pt, When modified Gram-Schmidt generates a well-conditioned set of vectors, IMA Journal of Numerical Analysis, 22 (2002), pp. 521-528.

14

L. GIRAUD, L. JUCIEN, AND R. MIRO, On the round-off error analysis of the Gram-Schmidt algorithm with reorthogonalization, Technical Report TR/PA/02/33, CERFACS, Toulouse, France, 2002.

15

A. GREENBAUM, V. PTÁK, AND Z. STRAKOš, Any nonincreasing convergence curve is possible for GMRES, SIAM J. Matrix Anal. Appl., 17 (1996), pp. 465-469.

16

A. GREENBAUM, M. ROZLOZNÍK, AND Z. STRAKOš, Numerical behaviour of the modified Gram-Schmidt GMRES implementation, BIT, 37 (1997), pp. 706-719.
Direct methods, linear algebra in optimization, iterative methods (Toulouse, 1995/1996).

17

M. J. GROTE AND T. HUCKLE, Parallel preconditioning with sparse approximate inverses, SIAM J. Sci. Comput., 18 (1997), pp. 838-853.

18

I. GUSTAFSSON, A class of first order factorization methods, BIT, 18 (1978), pp. 142-156.

19

W. HOFFMANN, Iterative algorithms for Gram-Schmidt orthogonalization, Computing, 41 (1989), pp. 335-348.

20

T. K. HUCKLE, Efficient computation of sparse approximate inverses, Numer. Linear Algebra Appl., 5 (1998), pp. 57-71.

21

S. A. KHARCHENKO, L. Y. KOLOTILINA, A. A. NIKISHIN, AND A. Y. YEREMIN, A robust AINV-type method for constructing sparse approximate inverse preconditioners in factored form, Numer. Linear Algebra Appl., 8 (2001), pp. 165-179.

22

L. Y. KOLOTILINA AND A. Y. YEREMIN, Factorized sparse approximate inverse preconditionings. I. Theory, SIAM J. Matrix Anal. Appl., 14 (1993), pp. 45-58.

23

C. LANCZOS, An iteration method for the solution of the eigenvalue problem of linear differential and integral operators, J. Res. Nat. Bur. Stand., 45 (1950), pp. 255-282.

24

J. A. MEIJERINK AND H. A. VAN DER VORST, An iterative solution method for linear systems of which the coefficient matrix is a symmetric 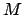${M}$-matrix, Math. Comp., 31 (1977), pp. 148-162.

25

N. M. NACHTIGAL, S. C. REDDY, AND L. N. TREFETHEN, How fast are nonsymmetric matrix iterations?, SIAM J. Matrix Anal. Appl., 13 (1992), pp. 778-795.
Iterative methods in numerical linear algebra (Copper Mountain, CO, 1990).

26

A. RUHE, Numerical aspects of Gram-Schmidt orthogonalization of vectors, Linear Algebra Appl., 52/53 (1983), pp. 591-601.

27

Y. SAAD AND M. H. SCHULTZ, Conjugate gradient-like algorithms for solving nonsymmetric linear systems, Math. Comp., 44 (1985), pp. 417-424.

28

G. L. G. SLEIJPEN, Gram-Schmidt orthogonalisation.
Personal notes, Januari 2000.

29

A. VAN DER SLUIS AND H. A. VAN DER VORST, The rate of convergence of conjugate gradients, Numer. Math., 48 (1986), pp. 543-560.

30

H. A. VAN DER VORST, Iterative methods for large linear systems.
Lecture notes on iterative methods, June 2002.

31

height 2pt depth -1.6pt width 23pt, Iterative Krylov methods for large linear systems, Cambridge University Press, Cambridge, 2003.
Cambridge Monographs on applied and computational mathematics, 13.