Partitioning a hypergraph using Mondriaan

This guide is a step-by-step introduction to using Mondriaan for the purpose of hypergraph partitioning. For more extensive information about Mondriaan, please take a look at the user's guide.

How to download and install Mondriaan

Download the latest version of Mondriaan. Uncompress with

This will create a directory Mondriaan4 which contains all the files of the Mondriaan package. Run

which will build Mondriaan and the associated tools.

Translating a hypergraph to the weighted Matrix Market file format

In order to use Mondriaan for hypergraph partitioning, it is necessary to convert your hypergraph to the Matrix Market file format and supply it with vertex weights. The hypergraph is interpreted as a matrix where there is a column for each vertex, and a row for each hyperedge or net.

Figure 1

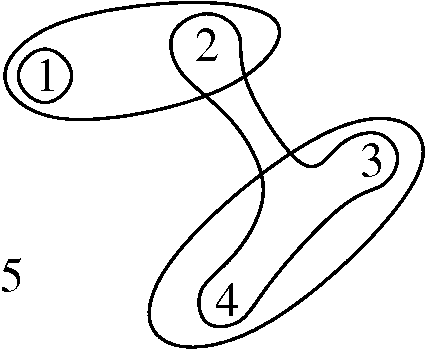
For example, we can consider the hypergraph G = (V, E) from Figure 1 with vertices V = {1, 2, 3, 4, 5} and nets E = {{1}, {1, 2}, {2, 3, 4}, {3, 4}} as a matrix A with 5 columns and 4 rows in Matrix Market format: 

%%MatrixMarket weightedmatrix coordinate pattern general
4 5 8 2 
1 1
2 1
2 2
3 2
3 3
3 4
4 3
4 4
1
1
1
1
1

Here the values 4 5 8 2 indicate that this is a matrix with 4 rows (nets), 5 columns (vertices), 8 entries (total number of vertices in all nets), and weighted columns (the value 2 equals 10 in binary: weighted columns, unweighted rows). Then after all nonzeroes, 1 1, 2 1, ..., we find the vertex weights, which are set to 1 for all five vertices.

Providing the vertex weights is essential, because otherwise Mondriaan will by default weigh all the columns by the number of nonzeroes contained in them, which will lead to unbalanced hypergraph partitions.

Setting the proper Mondriaan options

Now that we have our hypergraph as a Matrix Market file, say foo.mtx, we can use Mondriaan to partition it. First we go to the tools/ directory.

Here the options file Mondriaan.defaults should set SplitStrategy to onedimcol, because we want Mondriaan to partition the matrix columns, which correspond to the hypergraph vertices. Then we partition foo.mtx in two parts with a maximum imbalance of 10% by running

Extracting the hypergraph partitioning from the matrix partitioning

After performing the matrix partitioning, the file foo.mtx-v2 contains the vector distribution of the columns 

5 2
1 1
2 1
3 2
4 2
5 1

The first line 5 2 contains the number of columns (5) and the number of parts to which they have been assigned (2). Following this line are the column indices and the parts to which the columns have been assigned. Because the column indices correspond directly to the vertices of our hypergraph, we see that our hypergraph has been partitioned into two parts: {1, 2, 5} and {3, 4}, which was to be expected if you look at Figure 1.