1 Val en worp hebben in de loop van de geschiedenis velen bezig gehouden. Drie vragen komen daarbij telkens weer naar voren:
Het zijn vragen, die van zo essentieel belang voor het ontstaan der fysica zullen blijken te zijn, dat men welhaast kan zeggen, dat deze voor een aanzienlijk deel uit hun beantwoording gegroeid is. Voor het goed begrijpen van het verschil in karakter tussen de antieke en klassieke natuurwetenschap moet men eerst kennis nemen van wat Aristoteles (384-322 v. Chr.) over deze vragen te zeggen heeft (p. 27).
Aristoteles neemt aan (blijkbaar vertrouwend op de algemene geldigheid van verworven ervaringen) dat de gemiddelde snelheid over een zekere afstand evenredig is met de zwaarte van het vallend lichaam en omgekeerd evenredig met de weerstand van het medium (p. 28): v ~ G/W. (zie ook Dijksterhuis in Val en Worp op p. 18.)
Bovendien beschouwt Aristoteles het geval der gedwongen beweging. Een constante kracht geeft aan een lichaam waarop ze werkt een eenparige beweging. De snelheid van deze beweging is recht evenredig met de kracht, en omgekeerd evenredig met de zwaarte (traagheidsweerstand) van het lichaam (p. 30): v ~ K/W. Hierbij zag hij zwaartekracht niet als een kracht die van buitenaf op het lichaam werkt, maar een intrinsiek bewegingsprincipe. Het zou eeuwen duren voordat men de gecompliceerde samenhang ontward tussen traagheid en zwaartekracht en tussen massa en gewicht.
In de dertiende eeuw wordt door verscheidene scholastici de impetus-theorie ontwikkeld. Hierbij voert men ter verbetering van de worptheorie het begrip impetus of inwendig bewegend vermogen in (p. 197). Deze theorie verklaart als volgt hoe het komt dat een valbeweging met een groeiende snelheid verloopt: de zwaarte, aanvankelijk alleen werkend, doet het lichaam niet alleen vallen, maar deelt er ook een impetus aan mee, die het nu met haar samen voortbeweegt; daardoor wordt de beweging sneller en dus de impetus groter; het lichaam, bewogen door een constante zwaarte en een steeds groeiende impetus, zal zich dus steeds sneller gaan bewegen (p. 200).
De impetus beschouwt men hier dus enerzijds als gevolg en anderzijds als mede-oorzaak van de valbeweging. Aan het eind van een tijdvak Dt, dat begonnen is toen het lichaam werd losgelaten, heeft het lichaam een snelheid v; het bezit daardoor een impetus mv. Als nu de zwaartekracht ophoudt met werken dan beweegt het lichaam verder eenparig met snelheid v. Doordat echter de zwaarte blijft werken brengt ze in het volgende tijdvak Dt weer een snelheid v teweeg. Daardoor groeit de impetus tot 2mv, dat wil zeggen het lichaam bezit thans het vermogen om uit eigen kracht een eenparige beweging met snelheid 2v uit te voeren, enzovoort (Buridan). Het blijft hier echter duister wat in het eerste tijdvak gebeurt. Hier schuilt een essentiële moeilijkheid van het bewegingsbegrip: wij kunnen ons geen voorstelling vormen van het begin van een beweging. De klassieke mechanica springt bij de behandeling van de vrije val als het ware over deze moeilijkheid heen door te zeggen, dat de constante zwaarte direct een constante versnelling veroorzaakt. Om daaruit dan de eigenschappen van de beweging af te leiden is een zaak van redeneren, niet van voorstellen. Deze scholastici zijn echter niet zover gekomen om te concluderen dat de verworven snelheid evenredig is met de tijd. Slechts Albert van Saksen probeert een valwet te formuleren (die zich echter niet zoals de redenering van Buridan in de klassieke mechanica laat inpassen) waar verondersteld wordt dat de snelheid evenredig kan zijn met de doorlopen weg. Deze valwet zal later nog vaak als de meest voordehandliggende onderstelling worden uitgesproken, totdat Galileï na aanvankelijk door haar te zijn bekoord, haar ondenkbaarheid zal aantonen (p. 204).
In de veertiende eeuw begint het gebruik van letters voor berekeningen en breekt de tijd van de Calculatores aan (p. 208). Een mooi voorbeeld is dat van Thomas Bradwardine uit zijn Tractatus van 1328. Het probleem dat hij bestudeerde is, hoe de snelheid v van een mobiel, dat in beweging wordt gehouden doordat een kracht K de weerstand W overwint, bij verandering van de verhouding K/W verandert. Het lijkt dat hij hier direct de (niet zo geformuleerde) formule van Aristoteles kan gebruiken: v is recht evenredig met K en omgekeerd evenredig met W, met de conditie K > W. Bradwardine verwerpt echter deze evenredigheid. Ten eerste omdat men er volgens hem niet uit kan afleiden, wat er gebeurt als K en W gelijktijdig veranderen. Hij mist namelijk het begrip van samengestelde evenredigheid! En ten tweede omdat men hieruit zou kunnen afleiden dat iedere willekeurig kleine kracht ieder willekeurig zwaar lichaam in beweging kan brengen. En de ervaring leert dat dat niet het geval is (hier is de ervaring eerder misleidend dan verhelderend). Zijn theorie is gebaseerd op de middeleeuwse verhoudingsleer. In die verhoudingsleer wordt onder het optellen van verhoudingen verstaan, het vermenigvuldigen van de breuken. Terwijl het vermenigvuldigen van een verhouding met een getal n, betekent dat de representerende breuk tot de n-de macht verheven moet worden. Bradwardine beweert nu dat de snelheid de verhouding K : W volgt. Dat wil zeggen dat als de verhouding n-maal zo groot wordt (Kn : Wn), dan wordt de snelheid ook n-maal zo groot (n.v). In moderne notatie: v ~ log( K/W). Het voordeel hiervan is volgens Bradwardine, dat als er bij een gegeven verhouding K/W een beweging optreedt, dat je dan die verhouding door ieder willekeurig getal n kan delen zonder dat er een geval kan optreden waarbij geen beweging ontstaat. Immers als K/W > 1, dan is ook (K/W)1/n > 1. Als in de betrekking van Aristoteles de snelheid n-maal zo klein moet worden, dan moet je W n-maal zo groot maken. Maar het kan best zijn dat dan n.W > K en dat betekent dat de betrekking niet gebruikt mag worden.
Het gaat hier om een uit de lucht gegrepen mathematische formulering van een natuurwet, die getuigt van een zoeken en tasten naar een onderstelde afhankelijkheid, waarin een behoefte aan precisiering van een in de natuur vermoede wetmatigheid tot uiting komt. Ze is leerzaam als symptoom van de grote moeilijkheden die overwonnen zouden moeten worden, voordat men erin zou slagen de verschijnselen der natuur in de taal der wiskunde te beschrijven. Die moeilijkheden kwamen niet alleen voort uit onjuiste fysische onderstellingen, maar ook door eigenaardigheden en tekortkomingen van de wiskundige taal (vooral die van de Elementen van Euclides, ca 300 v. Chr.). Zo was het onmogelijk om over snelheid te spreken als verhouding van een weg tot een tijd (het quotiënt van de eenheden van weg en tijd is precies de eenheid van snelheid). In de Euclidische wiskunde kan men alleen van de verhouding van twee gelijksoortige grootheden spreken (zoals K en W). Nog eeuwen lang zal de mechanica zich door deze Euclidische beperking, in de ontwikkeling van haar uitdrukkingswijze belemmerd zien. (p. 212)
In de aanvankelijk zuiver aritmetische-algebraïsche wetenschap der Calculatores komt door toedoen van Oresme in de veertiende eeuw een nieuw element: die van de grafische voorstelling. Oresme was scholasticus, stierf als bisschop van Lisieux in 1382 en was volgeling van Willem van Ockham. Zoals menig geleerde in die tijd was hij natuurwetenschapper, schreef ook over muziektheorie en bestudeerde ars magica. Voor de bewegingsleer was zijn doel om een aanschouwelijke voorstelling te geven van de reeds lang bekende begrippen van de verandering van (niet-)eenvormige kwaliteiten, zoals temperatuur, gevoelens, charitas die als een werking van den H. Geest werd beschouwd, schoonheid, maar ook snelheden. Vooral bij het laatste onderwerp is Oresme's bijdrage aan de kinematica vruchtdragend geweest. Hij bestudeerde de snelheid afhankelijk van plaats in het object (bijv. bij een rotatie) en afhankelijk van tijd. We beperken ons hier tot het tweede geval. De longitude stelt nu het tijdvak voor waarin de beweging plaatsvindt, de latitudo wordt de instantane snelheid beschouwd als intensiteit van de beweging (er is maar één longitudo bij oneindig veel latitudo's) (p. 214).
Oresme kon eenparige bewegingen voorstellen middels rechthoeken. Hij identificeerde de afgelegde weg (of de kwantiteit van een beweging) als de oppervlakte van de rechthoek. Zo kon hij verschillende snelheden vergelijken middels verhoudingsstellingen. Om nu difforme snelheden te vergelijken moest hij die eerst omzetten in rechthoeken. Hij concludeerde dat een eenparig versnelde beweging (uniforme difforme kwaliteit) eenzelfde kwantiteit heeft als een eenparige beweging met een snelheid, die gelijk is aan de snelheid van de versnelde beweging op het middelste ogenblik m van het beschouwde tijdvak t.
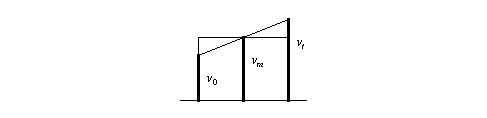
Uit zijn benadering van kinematische vraagstukken blijkt bovendien dat Oresme goed in de gaten had dat de maat vm . t de afgelegde weg in tijdvak t voorstelt. Daarmee kunnen we de formule voor de afgelegde weg aan Oresme toeschrijven:
Het betekenis geven aan de oppervlakte van alle latitudes is misschien ongeoorloofd, maar Oresme deed het (p. 217). Het is bovendien zo dat Oresme (en zijn tijdgenoten, zelfs tot en met Galileï) niet precies instantane snelheid konden definiëren. Ze beschreven haar als de snelheid der eenparige beweging die zou ontstaan als het object vanaf het beschouwde ogenblik zo door zou gaan als het juist bezig is te doen. En dat is een cirkelredenering, immers, op de vraag wat zo betekent, kan niet anders worden geantwoord dan door te zeggen: met de snelheid van het beschouwde ogenblik. Verbazend is verder dat noch Oresme, noch een van zijn tijdgenoten op het idee is gekomen om de regel toe te passen op de vrije val (hoewel wel het vermoeden wordt uitgesproken).
Tot slot wordt over Oresme opgemerkt dat hij de impetus-theorie gebruikt om een verklaring te geven voor het verschijnsel dat nog lang als reëel verschijnsel wordt beschouwd van de initiële worpversnelling: bij het weggooien van een voorwerp geef je het niet alleen een snelheid, maar ook een versnelling mee. Dit leidt tot de algemene overtuiging dat bij een worp het projectiel na verloop van twee fasen (versnelling bereikt maximum, versnelling bereikt nul) verticaal omlaag valt.
Oresme was dus niet de eerste die de regel voor de afgelegde weg formuleerde, maar hij gaf de regel de aanschouwelijkheid en vatbaarheid voor uitbreiding die haar waarlijk vruchtbaar zou maken. (p.219)
In de vijftiende en zestiende eeuw - de renaissance - ziet men in verschillende landen een klasse van practici ontstaan die, voor zover ze zich niet zelf met vragen van natuurwetenschappelijke aard bezig hielden, door de aard van hun werk die vragen bij anderen hebben doen rijzen (Brunelleschi, Ghiberti, Leonardo da Vinci, Dürer). (p. 266) Men kan vooral in Italië in de vijftiende eeuw een groeiend besef van de betekenis van de wiskunde als grondslag of essentieel hulpmiddel voor alle technische en artistieke werkzaamheid vaststellen.
Bijvoorbeeld Leonardo da Vinci (1452-1519): "De mechanica is het paradijs der mathematische wetenschappen, want door haar komt men tot de mathematische vrucht." Hij is interessant omdat uit al zijn aantekeningen blijkt hoe hij worstelde met begrippen als kracht, gemiddelde en instantane snelheid en beweging. Er bestaan allerlei interpretaties van zijn werk, die hem daardoor meer of minder lof doen toekomen. Uit zijn aantekeningen blijkt nog eens wat een der meest fundamentele moeilijkheden was die de mechanica moest overwinnen. Die moeilijkheid bestaat uit de noodzaak, voor een grootheid die van de tijd afhangt, een scherpe begripsbepaling te vinden ter fixering van de wijze, waarop ze op een gegeven moment bezig is te veranderen. Ofwel voor een beweging te zeggen wat men onder snelheid op zeker ogenblik verstaat. Het is niet moeilijk in te zien waarom het zo lang heeft moeten duren voordat men deze problemen heeft leren oplossen. Er zit iets paradoxaals in, te willen aangeven, hoe een grootheid op een zeker tijdstip bezig is te veranderen, terwijl het begrip verandering noodzakelijk vereist dat er een zeker tijdvak verloopt. Dit stelt ons ook in staat om de praktische betekenis van Oresme grafische voorstelling te beseffen. Een raaklijn en haar richting laten zich intuïtief duidelijker voorstellen dan de limiet van een differentiaal quotiënt, waarvan teller en noemer beide tot nul naderen. De grafische voorstelling schiep dus de mogelijkheden om aanschouwelijk te maken en op grond daarvan kinematische inzichten te verwerven die langs de weg van de analyse nog onbereikbaar waren.
Een der drempelwaarden van de nieuwe tijd is 1586, wanneer Simon Stevin (1548-1620) de Beghinselen der Weeghconst publiceert. Dit werk is echter vooral geweid aan de statica. Aan de vernieuwing van de dynamica heeft hij slechts terloops, maar niet zonder historische betekenis, een bijdrage geleverd. Samen met zijn vriend Johan Cornets de Groot (vader van Hugo de Groot) heeft hij een proef gedaan ter controle van de in de valwet van Aristoteles opgesloten bewering, dat de valtijd omgekeerd evenredig is met het gewicht van het vallende lichaam. Zij lieten twee loden bollen, waarvan de ene tien keer zo zwaar is als de andere, gelijktijdig van een hoogte van 30 voet op een plank vallen en gingen na, of de zwaarste bol inderdaad tien maal zo snel beneden was als de lichtste. Het verschil in tijd bleek onwaarneembaar te zijn; het was of men één slag hoorde. De proef staat in de Weeghkonst beschreven. Al eerder was proefondervindelijk aangetoond dat de valwet van Aristoteles strijdig was met de ervaring. Deze herhaalde poging was echter niet overbodig, omdat Aristoteles' dynamica nog steeds het denken van mechanici en astronomen in sterke mate beheerste (sterker dan zij zich konden en wij ons kunnen voorstellen). (p. 363)
De vernieuwing van het natuurwetenschappelijk denken in de zestiende en zeventiende eeuw bestaat voor een belangrijk deel uit de hervorming van de dynamica en deze weer in een diepgaande wijziging van de denkbeelden over val en worp. De centrale figuur in de geschiedenis van dit onderwerp is Galileï en we zullen dus, om de lijn Stevin-Huijgens te vervolgen, tijdelijk ons land moeten verlaten en terugkeren naar Italië. Maar niet direct, eerst zullen we het werk bekijken dat hier ten lande wordt verricht door Isaac Beeckman (1588-1637) 2 . Beeckman is net als Leonardo da Vinci tekort geschoten in het systematiseren, afronden en publiceren van zijn werk. Daardoor hebben ze de ontwikkeling der wetenschap niet of nauwelijks bevorderd. Wat we meedelen heeft waarde als indruk van het natuurwetenschappelijk denken van een begaafd man in het begin van de zeventiende eeuw. Het belangrijkste wat hij gedaan heeft, voor ons doel, is een dynamische afleiding geven van het verband tussen weg en tijd in de valbeweging, die hij in 1618 in samenwerking met Descartes gevonden heeft. Dit is de oudste bekende poging om het verloop van de val in verband te brengen met de zwaartekracht. (p. 364)
Zijn meetkundige redenering ging als volgt. Denk de zwaartekracht als iets dat niet doorlopend werkt, maar zo, dat ze telkens na verloop van een zeker tijdvak een rukje geeft aan het vallend lichaam. Verder nemen we aan dat een eenmaal voortgebrachte snelheid onveranderd blijft voortbestaan zolang er geen uitwendige oorzaken zijn die haar vernietigen. Zetten we nu op de vertikale as de tijd uit, en stel dat bij het begin van de beweging en dan verder telkens na een tijdvak t een snelheid g wordt voortgebracht, dan geeft de figuur de afgelegde wegen weer in totale tijdvakken OA 1 en OA 2 .
Als nu t tot nul nadert, dan worden de in deze tijdvakken afgelegde wegen voorgesteld door de driehoeken OA 1 B 1 en OA 2 B 2 . Deze verhouden zich als de kwadraten van OA 1 en OA 2 .
In moderne formulering: in het eerste tijdvak t wordt een weg van g t voortgebracht, in het tweede een weg van 2g t , in het derde 3g t , enzovoort. In een tijdvak t 1 = n . t wordt dus afgelegd:
s(t 1 ) = g t ( 1+ 2 + 3 + . . . + n) = g t . n ( n + 1) / 2
In het tijdvak t 2 = m . t wordt afgelegd:
s(t 2 ) = g t ( 1+ 2 + 3 + . . . + m) = g t . m ( m + 1) / 2
Voor de verhouding van deze wegen vindt men:
s(t 1 ) : s(t 2 ) = n ( n + 1) : m ( m + 1) = ( t 12 + t 1 t ) : ( t 22 + t 2 t )
Wanneer nu t tot nul nadert, gaat het trekken in rukjes over in een continue krachtwerking en de verhouding der wegen wordt:
s(t 1 ) : s(t 2 ) = t 12 : t 22
We hebben al uitgelegd dat men dit in de zeventiende eeuw nog niet kon formuleren als s(t) = c . t 2.
Deze redenering vertoont veel verwantschap met die van Oresme. Toch zijn er enkele kenmerkende verschilpunten. Ten eerste heeft Beeckman het nergens over instantane snelheid, en dus ook nergens zegt dat die door de horizontaal uitgezette ordinaat bij de extensio tijd wordt voorgesteld. Het verband met de leer van de intensio en remissio van kwaliteiten is dus geheel verdwenen. Ten tweede is nieuw de onmiskenbare invloed van Archimedes. Zijn werk is in de zestiende eeuw door vertaling bekend geworden en in het bijzonder zijn methode van zwaartepuntsbepaling. Deze berustte ook op een benadering van een figuur door een reeks rechthoeken als in bovenstaande afleiding. Beeckman heeft dit misschien van Descartes overgenomen, hij kan het echter ook gelezen hebben in Stevin's Weeghkonst.
Beeckman kon zich geen voorstelling maken van een inwendig bewegingsprincipe, de impetus volgens de Parijse Terministen, en wijst daarom deze theorie af. Hij zocht de verklaring in een uitwendig bewegingsprincipe. Bovendien nam hij een andere positie in ten aanzien van het causaliteitsbeginsel. De Terministen wensten, net zoals Aristoteles, een oorzaak voor beweging te zien: "geen plaatsverandering zonder oorzaak". Terwijl Beeckman in de traditie van de klassieke natuurwetenschap stelde: "geen snelheidsverandering zonder oorzaak". Dit is een merkwaardig verschil in zienswijze en het allermerkwaardigste is dat elk der beide standpunten voor beide partijen iets vanzelfsprekends blijkt te kunnen aannemen. De eerste is binnen het kader van de Aristotelische natuurfilosofie houdbaar, omdat plaats wordt opgevat als een absolute eigenschap van een lichaam en niet als een relatie tot een omgeving die ook veranderen kan. De tweede is echter niet volgens de eigen denkbeginselen van de klassieke mechanica te verklaren. Waarom moet de snelheid zonder oorzaak constant blijven en niet de versnelling of de kromming van de baan? Als men het evident wil vinden dat van een object dat plotseling aan alle invloeden van buitenaf onttrokken wordt, de snelheid in richting en grootte onveranderd zal blijven, dan kan men het evengoed evident vinden dat een lamp blijft branden als men de toevoerdraden voor de stroom doorknipt. Inderdaad zien we Beeckman ook beweren dat een lichaam dat bezig is cirkels te beschrijven, bij afwezigheid van alle uitwendige invloeden, dat ook zal blijven doen. (p. 367)
Galileo Galileï (1564-1642) schreef in zijn eerste publikaties ook over de valbeweging. Z'n redeneringen zijn dan nog nauw verwant met die van de Parijse Terministen. Bij een worp zal zodra de val begint de beweging versnelt zijn zolang de vis impressa (impetus) tijd nodig heeft om geheel te verdwijnen (vanuit rust vallend is de vis impressa gelijk aan het gewicht van het object). Daarna zal die onder invloed van de constante zwaarte eenparig verlopen, vanaf het zogenaamde eenparigheidspunt. Bij Beeckman treffen we eenzelfde begrip aan, bij hem ligt de oorzaak echter in het met de snelheid aangroeien van de luchtweerstand, terwijl bij Galileï het eenparigheidspunt ook in een vacuum bestaat.
In een later stadium van zijn ontwikkeling geeft Galileï aan dat het verschil der valsnelheden voor lichamen van verschillend soortelijk gewicht kleiner zal zijn naarmate het medium ijler is; het is dus redelijk om te verwachten dat dit verschil in een vacuum verdwenen zal zijn. Dit vermoeden wordt op de proef gesteld door valproeven op een hellend vlak met een kleine hellingshoek. In een formule uitgedrukt:
Hierin staat v voor de gemiddelde snelheid over een zekere weg (omdat de lengte van die weg niet wordt opgegeven, blijkt dat er nog niet wordt gelet op het feit dat de valbeweging versneld is), S het soortelijk gewicht van het vallend lichaam en S m van het medium, terwijl de evenredigheidsfactor kennelijk staat voor de valsnelheid in een vacuum. Tot dusver staat Galileï dus nog aan de middeleeuwse kant van de grenslijn tussen de oude en de nieuwe natuurwetenschap. Al behoort hij daar wel tot de critici van Aristoteles. Een van de oorzaken dat hij niet aan die kant gebleven is, is de mathematische inslag van zijn denken (onder invloed van Archimedes). (p. 372) Deze inslag heeft hem er toe gebracht om in het heersende meningsverschil van zijn tijd over de juiste methode van de natuurwetenschap, de Platonische richting te verkiezen boven de Aristotelische. De Platonische richting ziet wiskunde als essentieel bestanddeel van natuuronderzoek, terwijl de Aristotelische richting wiskunde slechts als hulpmiddel ziet: de beschouwing van het kwalitatieve van verschijnselen is belangrijker dan het opsporen van kwantitatieve relaties.
Uit de gesprekken die in de Dialogo gevoerd worden blijkt zijn nieuwe aanpak van de val en worp. Het gaat dan om de oorzaak waardoor lichamen naar de aarde worden gevoerd. Dan antwoordt de vertegenwoordiger van de Aristotelische filosofie dat iedereen toch weet dat dit de zwaarte is. Waarop Salviati (die voor Galileï spreekt) antwoordt dat hij had moeten zeggen dat iedereen weet dat dit de zwaarte heet. Dit is de zere plek van de Aristotelische natuurfilosofie. De illusie dat wij alleen door namen te geven, onze feitelijke kennis van de natuur zouden kunnen uitbreiden. (p. 550: Het substantiële denken, dat naar het wezen der dingen vroeg, moet worden verruild voor het functionele, dat de gedragingen der dingen in hun onderlinge afhankelijkheid wil vaststellen, de behandeling der natuurverschijnselen in woorden worden opgegeven voor een mathematische formulering van de daarin waargenomen relaties.) Galileï trekt als conclusie dat het tijd is om met namen te geven op te houden. Men mag blijven zeggen dat de valbeweging toe te schrijven is aan de werking van een natuurlijk streven naar het aardcentrum, mits men niet teveel over dat streven spreekt waarvan we verder niets weten. Laten we eerst de moeite nemen de val zelf, die we kunnen waarnemen beter te leren kennen. Hiermee schakelt Galileï de dynamische beschouwingswijze uit en beperkt zich tot de kinematische. (p. 373)
Galileï maakt ook gebruik van grafieken om het kwadratische verband tussen afgelegde weg en tijd aan te tonen. In de grafiek hieronder heeft hij de snelheid-tijd grafieken van twee situaties weergegeven. AC geeft de eenparig versnelde beweging weer en FG de beweging met een constante snelheid van het middelste ogenblik M.
Grafiek van Galileï uit Discorsi III 1 (Opere VIII 208).
De redering van Galileï verschilt echter van die van Oresme. De redering van Galileï gebruikt de verzameling van momentane snelheden (die hij niet helemaal correct kon definiëren). In plaats van oppervlaktes als maat voor de afgelegde weg, bekijkt Galileï alle lengtes cc 1 , en dd 1 die bij elkaar de totale snelheid weergeven waarmee de weg doorlopen wordt. Omdat deze lengtes symmetrisch rond M liggen en overal geldt cc 1 + dd 1 = cc 2 + dd 2 , leidt hij uit deze grafiek af dat ook de afgelegde wegen gelijk zijn. Hieruit leidt hij de kwadratenwet af, waarbij hij opnieuw niet over oppervlaktes spreekt, en vervolgens de wet der oneven getallen (de wegen in opvolgende gelijke tijden verhouden zich als de opvolgende oneven getallen). (p. 379)
Men is het op een gegeven moment didactisch wenselijk gaan vinden om de kwadratenwet als het ware af te lezen uit waarnemingen van weg en tijd, en ging toen vanzelfsprekend vinden dat Galileï ook zo te werk moest zijn gegaan. Dit is echter niet alleen feitelijk onjuist, maar ook strijdig met zijn methodische beginselen. Hij experimenteert niet om een natuurwet op het spoor te komen, maar om een relatie die hij door mathematische redenering uit min of meer evident lijkende onderstellingen heeft afgeleid, achteraf te verifiëren. (p. 380)
Bij Galileï is er sprake van een tweeledige methode van natuurwetenschappelijk onderzoek. Ten eerste de methode der analyse, het gissend opsporen van oorzaken bij verschijnselen, en ten tweede de methode der synthese, het geven van het bewijs dat die verschijnselen inderdaad uit die oorzaken voortvloeien. (p. 259)
Tot slot: De mechanisering, die het wereldbeeld bij den overgang van antieke naar klassieke natuurwetenschap heeft ondergaan, heeft bestaan in de invoering van een natuurbeschrijving met behulp van de mathematische begrippen der klassieke mechanica; zij beduidt het begin van de mathematisering der natuurwetenschap, die in de physica der twintigste eeuw haar voltooiing krijgt. (p. 550)
De reflexieve relatie tussen symbool/theorie/begripsontwikkeling uit contexten en je kennis over contexten laat zich ook illustreren door (p. 206): had Ockham de beschikking gehad over onze natuurwetenschappelijke terminologie dan zou hij zich kunnen verdiepen in waarom kwaliteiten verschillen. Nu antwoordt hij op de vraag naar verschillen (in temperatuur/lading/...) met: "Ik zeg, dat hiervoor geen andere grond bestaat dan dat de natuur van het ene zo en die van het andere anders is."
Overtuigingen betreffende de valbeweging (p.374):
In Dijksterhuis' Val en Worp (Noordhof: Groningen, 1924) staan nog twee reacties op Galileï. Ten eerste volgt hier Descartes' redenering die concludeert dat de (gemiddelde) snelheden over twee opvolgende gelijke wegen vanaf het begin der beweging zich verhouden als 1 : 3. Hij maakt daarvoor een grafiek waarbij (i.t.t. Beeckman) langs de vertikale as de afgelegde weg staat.
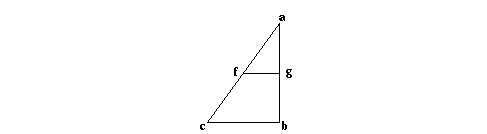
Als nu een steen in een vacuum van a naar b wordt getrokken door de kracht die steeds gelijkmatig van de aarde uitstroomt, blijkt het, dat de helft gb drie maal zo snel doorlopen wordt als de helft ag. Dit komt doordat de steen daar met een drie maal zo grote kracht wordt aangetrokken, het oppervlak fgbc is namelijk drie maal zo groot als het oppervlak afg. De oppervlakten geven gemiddelde snelheden aan.
De volgende redenering van Fermat bekritiseert de stelling van Galileï dat de snelheid van een uit rust vallend lichaam vanaf de waarde nul continu aangroeit (Descartes heeft ook deze stelling van Galileï verworpen).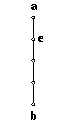
Een lichaam valt uit rust in a. "Nu krijgt het", aldus Fermat, "of in het eerste ogenblik een zekere snelheid, of in zekere tijd, bijvoorbeeld wanneer het in b is. Indien het snelheid krijgt op het eerste ogenblik, heeft het dus al snelheid wanneer het begint zich te bewegen. Immers, een ogenblik is ondeelbaar. Dit nu strookt met onze mening, en is in strijd met die van Galileï. Rest het geval dat Galileï zegt, dat de snelheid in zekere tijd verkregen wordt, b.v. wanneer het lichaam in b is. Dit impliceert echter een contradictie wegens de stellingen van Galileï zelf: zij be = 3 . ae, dan is volgens Galileï de snelheid van het lichaam in b twee maal zo groot als in e; dus heeft het lichaam in e een snelheid, in strijd met de onderstelling."
Descartes, die het wel eens is met de conclusie, kan deze redenering niet aanvaarden. Hij merkt op dat Fermat volgens deze redenering ook zal ontkennen dat in een driehoek de lengte van een lijn evenwijdig aan de basis bij nadering tot de top beneden iedere grens daalt.
Drie Aristotelische concepties die je ook bij leerlingen tegenkomt (volgens Weller in JSRT 32, pp 271, 1995) zijn:
Verwijzing naar Euclides m.b.t. denken in verhoudingen wordt ook beschreven door Janvier in verband met epistemologische obstakels (Mathematical Behavior 17 (1), p. 88, 1998).
1. Het volgende is niet echt een abstract, maar een samenvatting van voor de ontwikkeling van de kinematica relevante onderdelen. Af en toe heb ik citaten cursief afgedrukt, dat neemt niet weg dat de overige tekst vaak ook letterlijk is overgenomen.
2. In 1616 a man of position usually entered either the army or the church; Descartes chose the former profession, and in 1617 joined the army of Prince Maurice of Orange, then at Breda. Walking through the streets there he saw a placard in Dutch which excited his curiosity, and stopping the first passer, asked him to translate it into either French or Latin. The stranger, who happened to be Isaac Beeckman, the head of the Dutch College at Dort, offered to do so if Descartes would answer it; the placard being, in fact, a challenge to all the world to solve a certain geometrical problem. Descartes worked it out within a few hours, and a warm friendship between him and Beeckman was the result. (http://www.descarte.demon.co.uk/)
