[Next] [Previous] [Top]
Cabri
Versie: 2
Laatste update: 1996
Leverancier(s): CAN / Texas Instruments
Hardware specificatie: dos (vanaf xt)
Prijs enkelvoudig: ?
Prijs in licentie: ?
DOS/Windows/Windows95: dos (met windows-uiterlijk)
Overig materialen: Geïntegreerd in het experimentele materiaal van Profi. Verder is veel informatie op internet te vinden, onder andere via: Dynamic Geometry Software.
Essentie van het programma
Cabri is een programma voor de vlakke meetkunde. Het is een menu-gestuurd instrument voor het tekenen van meetkundige constructies. De kracht van het programma is de mogelijkheid om onderdelen van de constructie te bewegen, waarbij de eigenschappen van de constructie bewaard blijven.
Nadere informatie
- Uitgebreidere omschrijving
Met het programma kunt u figuren tekenen als punten, lijnen en cirkels. Bovendien is het mogelijk om dergelijke figuren te construeren afhankelijk van bestaande figuren; afhankelijk in de zin van `loodrecht op', `parallel aan', `door de drie punten...', etcetera. Zo is het alsof u met passer en lineaal construeert. Bij een meetkundige constructie in Cabri ontstaat dan een hiërarchie van afhankelijkheden. Bij het verplaatsen van onderdelen van de constructie blijven die afhankelijkheden bewaard (zie Deellijn en middelloodlijn). Hiermee is Cabri een middel om meetkundige vermoedens op het spoor te komen of aannemelijk te maken.
- Wiskundige mogelijkheden
- Het tekenen van punten, lijnen en cirkels.
-Het construeren van middens van lijnstukken, snijpunten van lijnen en cirkels, parallelle lijn aan gegeven lijn en door gegeven punt, spiegelbeeld, middelloodlijn, bisectrice, loodlijn, middelpunt, cirkel door drie punten, en dergelijke (zie De bissectricen-vierhoek).
- Het meten van lengten en hoeken. Als een onderdeel van een constructie verplaatst wordt, dan worden ook de aanwezige metingen aangepast.
- Het laten zien van de meetkundige plaats van een object. Met het programma kun je bijvoorbeeld een punt over een cirkel laten bewegen en vervolgens onderzoeken wat de meetkundige plaats is van een object dat met behulp van dat punt is geconstrueerd (zie Conflictlijnen).
- Toepassingen in het onderwijs
De vlakke meetkunde is een domein in het profiel N&T op het vwo. In dit profiel is Cabri een zeer goed hulpmiddel om leerlingen zelf meetkundige stellingen te laten ontdekken (zie Een bijzondere driehoek).
Daarnaast zijn in het domein meetkunde&analyse ook vele mogelijkheden om Cabri in te zetten (zie Conflictlijnen).
Voor de onderbouw is het mogelijk om in Cabri constructies te maken waarmee leerlingen kunnen werken om bijvoorbeeld eigenschappen van symmetriën te onderzoeken.
Bruikbaarheid in het curriculum


Toepasbaar in de vakken
Het is mogelijk om opstellingen uit de mechanica met Cabri na te bouwen en vervolgens meetkundige plaatsen of evenwichten van krachten te onderzoeken. Maar waarschijnlijk zal een dergelijk gebruik van Carbi eerder een toepassing van de wiskunde zijn in de wiskundeles, dan bij natuurkunde plaatsvinden.
Bruikbaar of in gebruik bij vervolgopleidingen
Cabri is zeker te gebruiken bij de wiskundestudie. Verder zijn er vooralsnog geen toepassingen bekend.
Voorbeelden
Deellijn en middelloodlijn
Teken een driehoek ABC, de deellijn van -C en de middelloodlijn van AB.
Teken ook de omgeschreven cirkel van driehoek ABC.
De deellijn en de middelloodlijn snijden elkaar (meestal) in een punt S.
Houd A en B vast en versleep punt C.
Waar ligt C als de deellijn en de middelloodlijn elkaar niet snijden?
Wat gebeurt er met het punt S als je C versleept? Formuleer een vermoeden.
Onderzoek wat er met punt S gebeurt als je de vorm van de driehoek verandert.
Formuleer een vermoeden.
Een bijzondere driehoek
Teken twee punten M en N. Teken de cirkel om M door N.
Kies op deze cirkel een punt A en teken de cirkel om N door A.
De twee cirkels snijden elkaar in een tweede punt B.
Kies op de cirkel om M een punt S en teken de lijnen SA en SB.
De lijn SA snijdt de cirkel om N nog in een punt T.
Je tekening moet nu dezelfde elementen bevatten als de figuur hieronder.
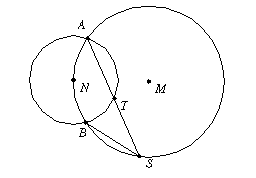
Driehoek STB heeft een bijzondere eigenschap. Welke?
Formuleer hieromtrent een vermoeden.
De bissectricen-vierhoek
Teken een willekeurige vierhoek ABCD. Teken ook de vier bissectrices.
De bissectrices sluiten een vierhoek PQRS in. Dit probleem gaat over de vorm van deze bissectricen-vierhoek.
Op het eerste gezicht heeft deze geen bijzondere eigenschappen. Om het probleem te verkennen gaan we dus eerst een paar bijzondere gevallen onderzoeken.
Schuif de punten A,B, C en D zo dat vierhoek ABCD (vrijwel) een parallelogram wordt. Formuleer voor deze situatie een vermoeden over de vorm van vierhoek PQRS.
Onderzoek ook wat er met de vierhoek PQRS gebeurt als ABCD de vorm heeft van:
- een rechthoek
- een ruit
- trapezium
Ook in het algemene geval heeft vierhoek PQRS een bijzondere eigenschap.
Misschien kun je zelf al een vermoeden formuleren.
Anders komt hier een hint: let op de hoeken van vierhoek PQRS!
Conflictlijnen
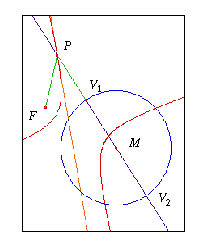
We onderzoeken eerst het geval `punt - rechte lijn'.
De stappen van de voorbereidingsfase en de constructiefase zijn reeds aan de orde geweest. De laatste drie stappen zijn bedoeld om de tekening zo duidelijk mogelijk te maken.

Voer deze constructie uit.
Versleep nu punt V en kijk wat er met punt P gebeurt. Dat punt doorloopt nu de conflictlijn. Let goed op driehoek FPV. Wat verandert wel en wat niet?
Met de optie Extra 1 > Animation kun je de computer als het ware als een flipperkast gebruiken. Kies deze optie en klik punt V aan. Als je nu de muis verplaatst zie je dat een veer gespannen wordt. Hoe verder je de muis verschuift hoe verder wordt de veer gespannen en hoe harder zal punt V langs lijn l schieten. Trek dus niet te hard!
Tot nu toe zie je steeds punt P bewegen maar je ziet nog niet de conflictlijn zelf.
Deze kromme maak je zichtbaar met de optie Construeer 1 > Locus.
Kies deze optie. Klik dan eerst op P en dan op V. De computer tekent nu de conflictlijn.
locus = plaats
Opmerking: `Locus' is het Latijnse woord voor `plaats'. Met de optie Locus laat je de plaats tekenen van alle punten P als V langs lijn l verschuift. Men spreekt ook wel van de `meetkundige plaats'.
Onderzoek nu hoe de vorm van deze conflictlijn verandert als je de afstand van F tot lijn l kleiner of groter maakt. Je kunt ook lijn l draaien en kijken wat er gebeurt.
Als je punt V versleept draait de middelloodlijn van FV.
Met de Locus-optie kun je ook veel standen van deze middelloodlijn laten tekenen.
Bedenk welke handelingen je moet doen en laat de computer ook nog deze locus tekenen.
Welke rol lijken deze middelloodlijnen voor de conflictlijn te spelen?
Onderzoek nu ook conflictlijnen van punt-cirkel en lijn-cirkel.
ICT-Wiskunde - 19 NOV 96
[Next] [Previous] [Top]
Generated with CERN WebMaker





