Grafen&Matrices

Laatste update: 1995

Leverancier(s): EPN

Hardware specificatie: dos-minimaal 386

Prijs enkelvoudig: f 150,-

DOS/Windows/Windows95: windows

Overig materialen: werkbladen, docentenhandleiding.

Essentie van het programma

Nadere informatie

1. Uitgebreidere omschrijving
   De volgende activiteiten zijn mogelijk:
   Het tekenwerk
   In een onderdeel van het scherm kun je een graaf tekenen. Eenvoudig kunnen punten of verbindingen toegevoegd en verwijderd worden. Ook is het mogelijk om de graaf te vervormen door punten te verplaatsen. Tegelijk zie je de gevolgen van je veranderingen in een verbindingsmatrix. Ook kan via deze verbindingstabel de graaf worden veranderd. In een graaf kun je routes aflopen waarbij de afstand van de afgelegde weg zichtbaar is.
   Het rekenwerk
   In het geval van de Leslie-matrices staan in de graaf de populatieklassen en de overgangen gegeven. Iedere populatieklasse heeft een bepaalde omvang. Met het programma kun je de omvang of de verdeling van de populatie in de loop der tijd berekenen. Eventueel kun je dat verloop in een grafiek weergeven (zie Een konijnenpopulatie).
   Machten van een verbindingsmatrix kunnen worden berekend. Naast de graaf is dan het verband met bijvoorbeeld meerstapswegen direct zichtbaar.
   De dynamiek
   Onder punt 1 is het verband tussen de graaf en de matrix reeds genoemd. Dit verband gaat echter verder. Stel je hebt een graaf en een bijhorende afstandstabel. Als je een verbinding uit de graaf verwijdert, dan zie je direct de gevolgen aan de veranderingen in de afstandstabel. Of bij de Leslie-matrices: je kunt iets aan het model veranderen en bekijken wat de gevolgen zijn voor de populatie, hoe de grafiek die het verloop van de populatie weergeeft verandert.
2. Wiskundige mogelijkheden
   Met het programma kun je doorloopbaarheid van grafen, centrale punten en verbindingen in grafen, kleurproblemen en markovprocessen onderzoeken.
3. Toepassingen in het onderwijs
   In de vwo profielen C&M en E&M wordt matrixrekening aan het onderwerp grafen en matrices toegevoegd. Dat betekent dat machten van matrices en matrix-vector vermenigvuldiging worden geïntroduceerd. Machten van verbindingsmatrices worden bijvoorbeeld gebruikt voor het onderzoeken van meerstapswegen in een graaf. Ook hierbij geldt dat het naast elkaar zien van de graaf en de verschillende machten een bijdrage aan het onderwerp levert. Tegelijk neemt het programma je veel rekenwerk uit handen. Nu kunnen ook meer ingewikkelde, vaak meer realistische toepassingen worden onderzocht. Voor overgangsmatrices gelden soortgelijke argumenten. Het doorrekenen van meer ingewikkelde modellen is nu mogelijk. Tevens biedt de mogelijkheid om je data in een grafiek bij te houden een extra invalshoek om het model te interpreteren en de situatie te onderzoeken. In de werkbladen staan een aantal voorbeelden die illustreren hoe het programma bij deze onderwerpen kan worden gebruikt.

Bruikbaarheid in het curriculum

Toepasbaar in de vakken

Voorbeelden

Een konijnenpopulatie

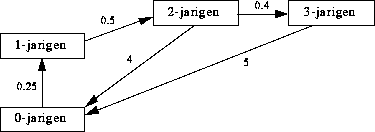
De getallen in de graaf worden mede bepaald door de jacht op de konijnen. Pas nadat de oudere konijnen geworpen hebben mogen zij afgeschoten worden. Jagers schieten niet op 0- of 1-jarige konijntjes.

1. Maak zelf de graaf (kies voor een gerichte graaf).
   A is 0-jarigen, B is 1-jarigen, enzovoort.
   
   Klik op de Info-button in het venster van de graaf.
   Zorg dat de labels van de punten zichtbaar zijn, èn dat er getallen in staan
   
   
   
   
   Nu staan er nullen in de labels! De beginpopulatie is
   Voer deze getallen in bij de labels.
   
2. Wat gebeurt na verloop van tijd met deze populatie konijnen?
   
   
   
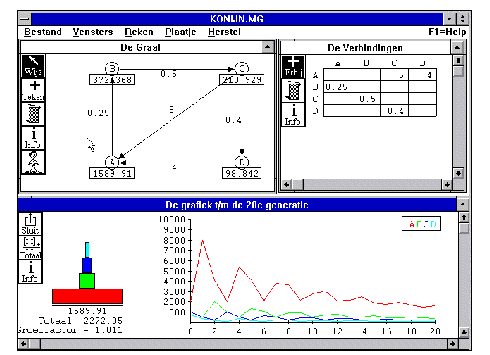
3. In de grafiek kun je ook alleen het totaal van de populatie weergeven. Klik hiervoor op de button Totaal in het grafiek-venster.
   (Gebruik Info om de grafiek goed in beeld te krijgen.)
   
   Hoe zou de grafiek lopen als deze populatie in evenwicht zou raken?
   

De boswachter merkt dat het slecht gaat met de konijnen. Hij leest dat als er niet gejaagd wordt, de overlevingskans van een 2-jarig konijn 0.9 is.
Als er helemaal niet gejaagd wordt ontstaat volgens de jagers een konijnenplaag.

1. Onderzoek met het programma of ze gelijk hebben.

Te downloaden voorbeelden

Generated with CERN WebMaker