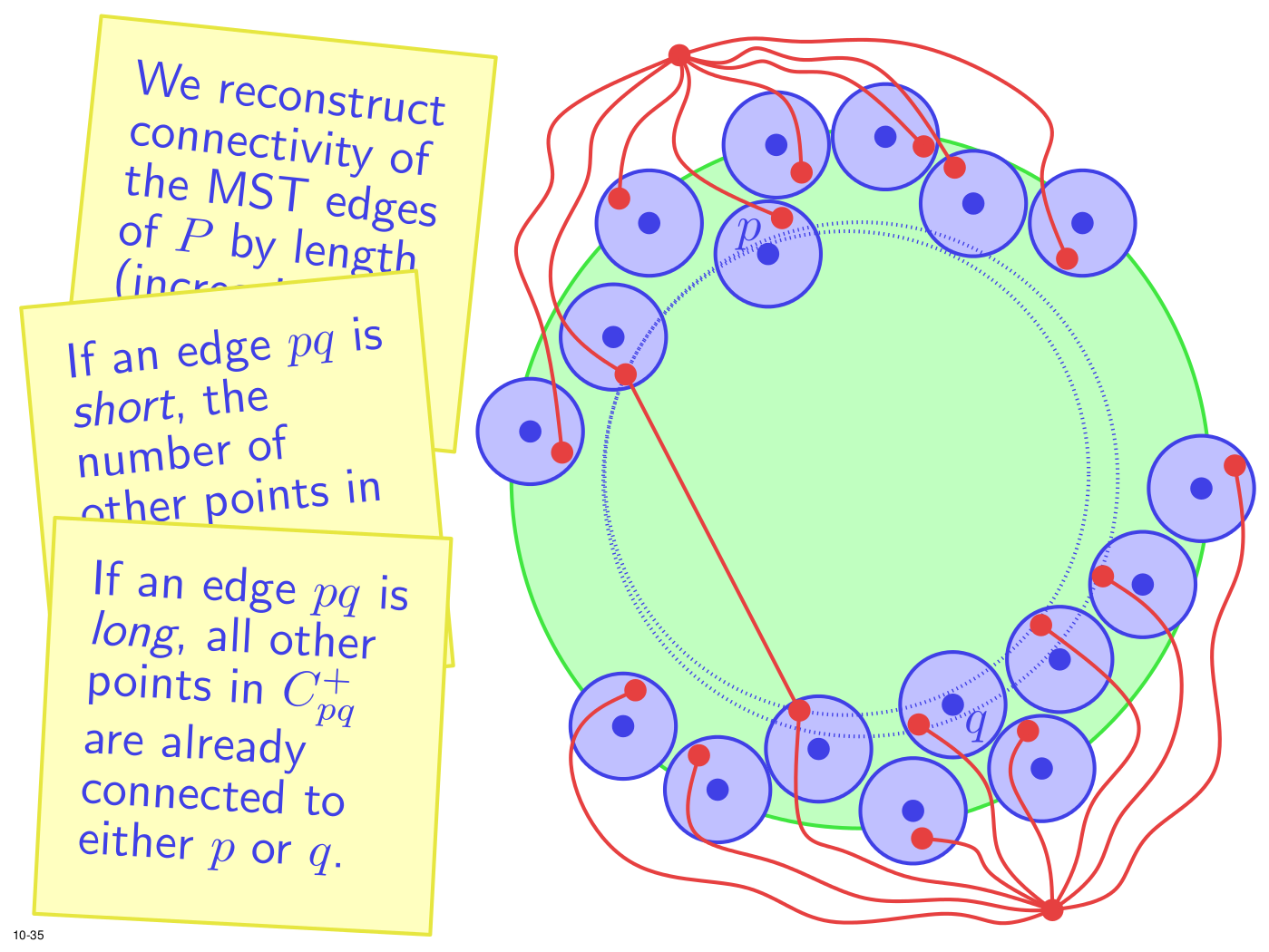
slides
An assumption of nearly all algorithms in computational geometry is that the input points are given precisely, so it is interesting to ask what is the value of imprecise information about points. We show how to preprocess a set of n disjoint unit disks in the plane in O(n log n) time so that if one point per disk is specified with precise coordinates, the Delaunay triangulation can be computed in linear time. From the Delaunay, one can obtain the Gabriel graph and a Euclidean minimum spanning tree; it is interesting to note the roles that these two structures play in our algorithm to quickly compute the Delaunay.