slides
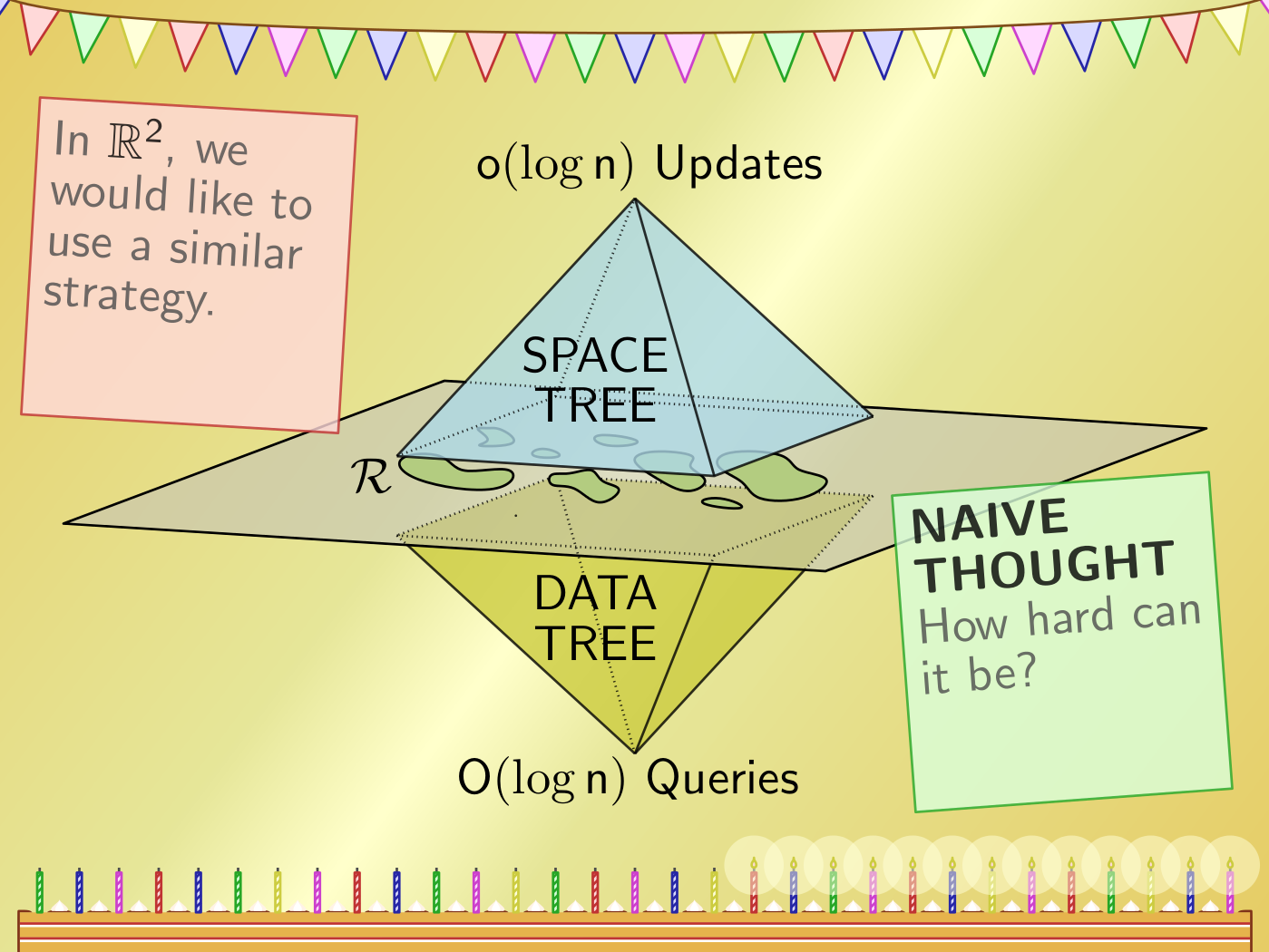
We study planar point location in a collection of disjoint fat regions, and investigate the complexity of local updates: replacing any region by a different region that is ``similar'' to the original region. (i.e., the size differs by at most a constant factor, and distance between the two regions is a constant times that size). We show that it is possible to create a linear size data structure that allows for insertions, deletions, and queries in logarithmic time, and allows for local updates in sub-logarithmic time on a pointer machine.