slides
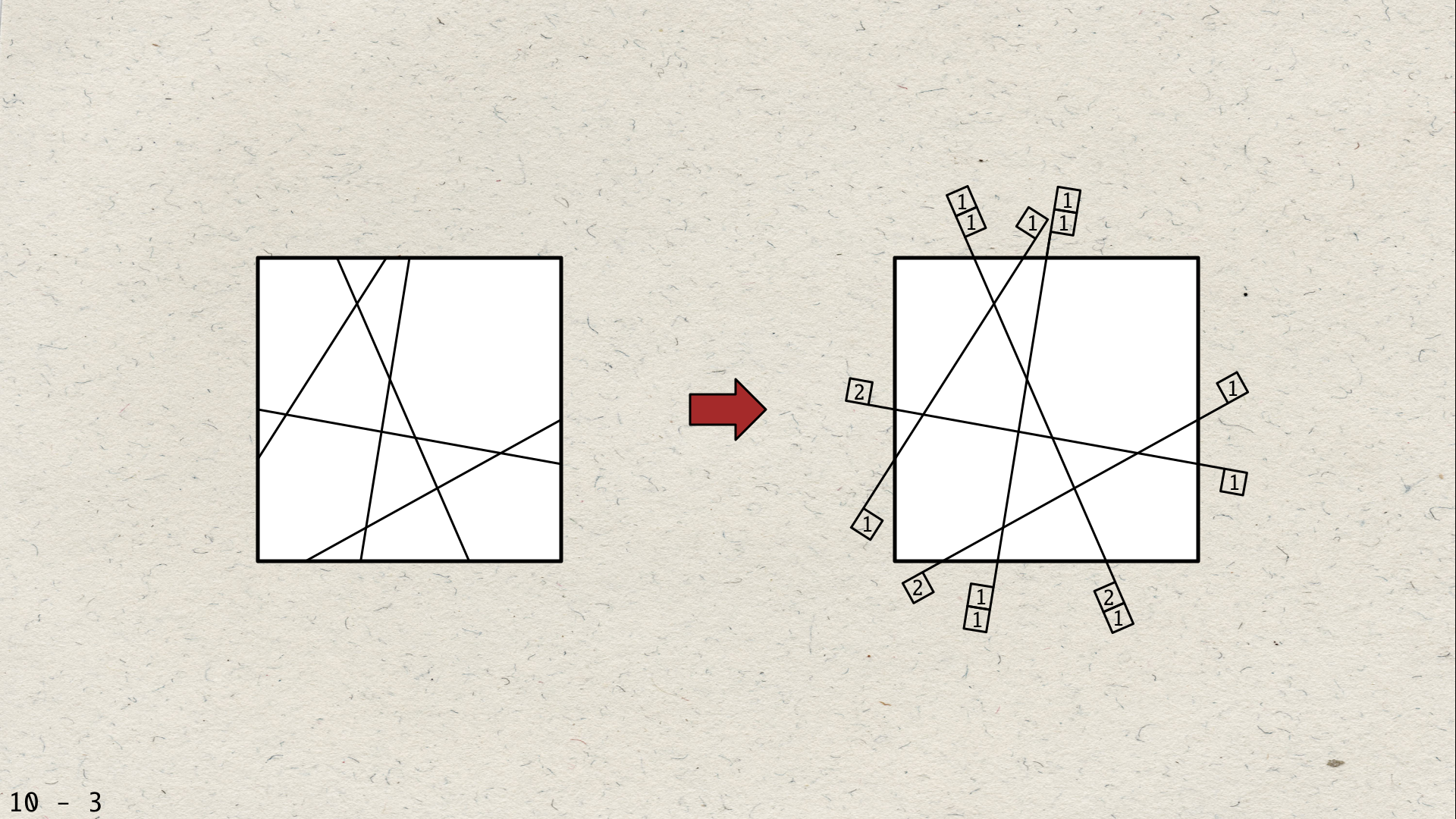
Slanted and curved nonograms are a new type of picture puzzles introduced by van de Kerkhof et al. (2019). They consist of an arrangement of lines or curves within a frame B, where some of the cells need to be colored in order to obtain the solution picture. Up to two clues are attached as numeric labels to each line on either side of B. In this paper we study the algorithmic problem of optimizing or deciding the existence of a placement of the given clue labels to a nonogram. We provide polynomial-time algorithms for restricted cases and prove NP-completeness in general.