Planar and Poly-Arc Lombardi Drawings

In Lombardi drawings of graphs, edges are represented as circular arcs and the edges incident on vertices have perfect angular resolution. However, not every graph has a Lombardi drawing and not every planar graph has a planar Lombardi drawing. We introduce k-Lombardi drawings, in which each edge may be drawn with k circular arcs; we show that every graph has a smooth 2-Lombardi drawing and every planar graph has a smooth planar 3-Lombardi drawing. We also investigate related topics connecting planarity and Lombardi drawings.

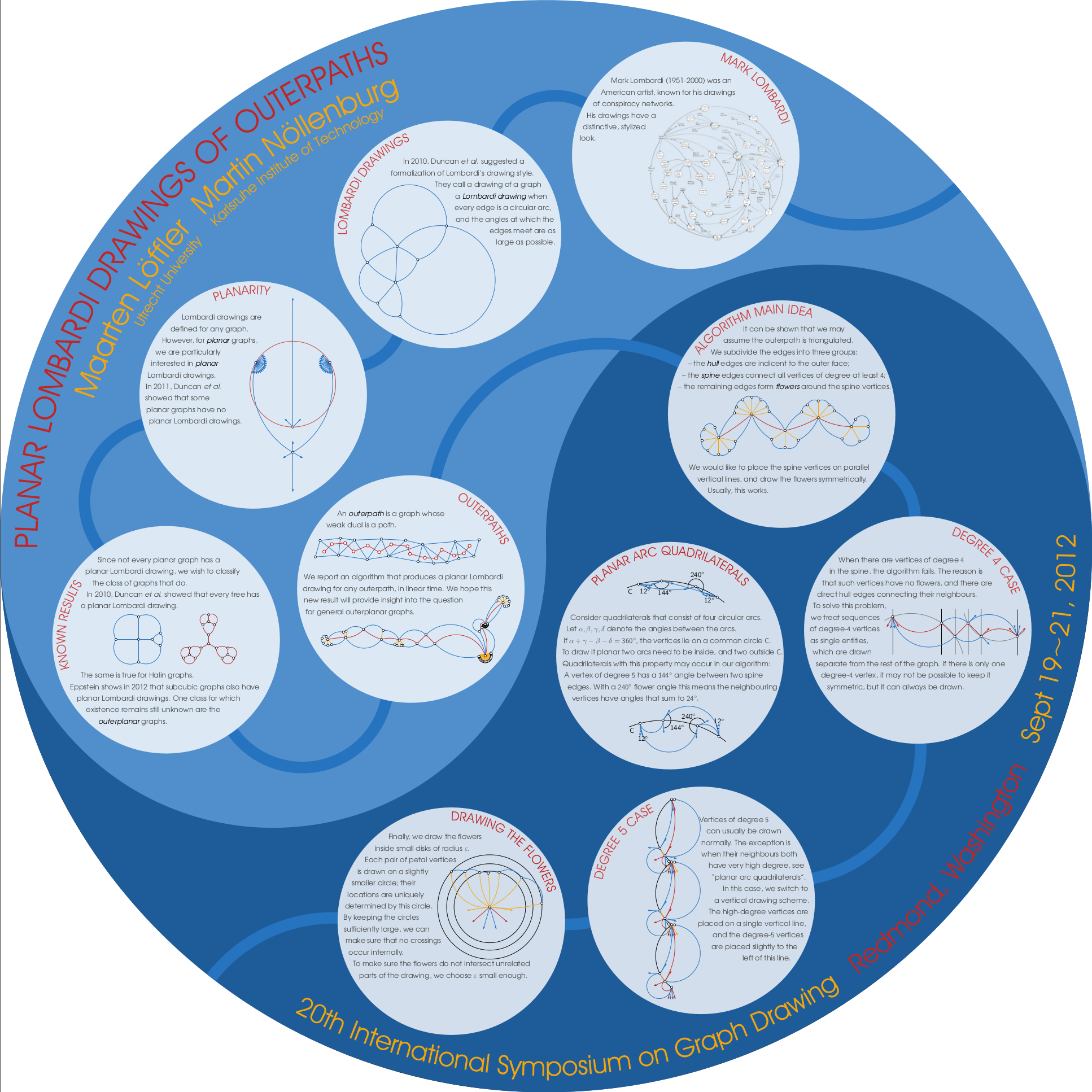
Lombardi drawings are drawings of graphs in the plane so that every edge is represented by a circular arc and every vertex has perfect angular resolution. We study planar Lombardi drawings for outerpaths, i.e., outerplanar graphs whose dual is a path. We show that every outerpath has an outerplanar Lombardi drawing and present a linear-time algorithm to construct it.