slides
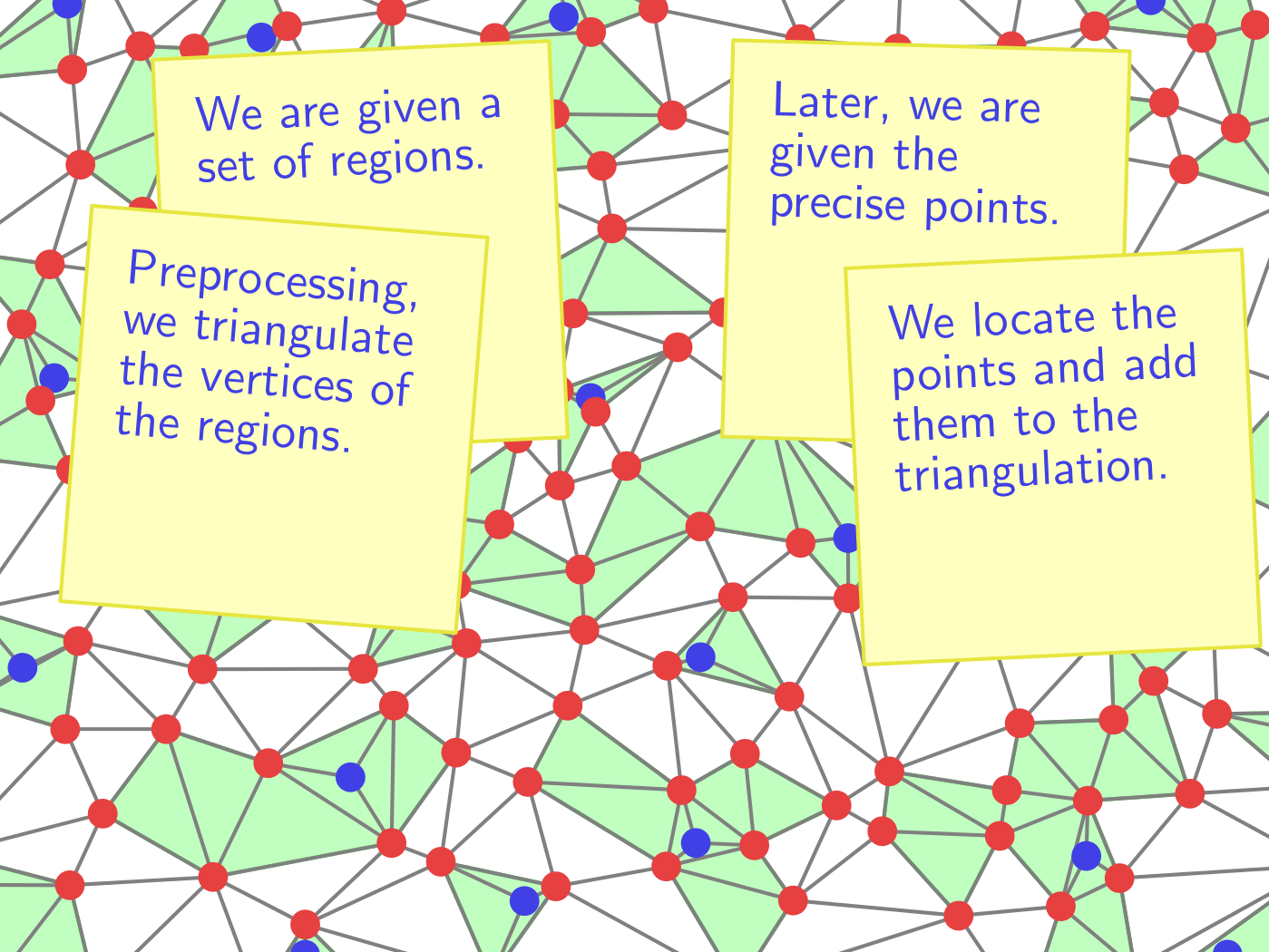
Traditional algorithms in computational geometry assume that the input points are given precisely. In practice, data is usually imprecise, but information about the imprecision is often available. In this context, we investigate what the value of this information is. We show here how to preprocess a set of disjoint regions in the plane of total complexity n in O(n log n) time so that if one point per set is specified with precise coordinates, a triangulation of the points can be computed in linear time. In our solution, we solve another problem which we believe to be of independent interest. Given a triangulation with red and blue vertices, we show how to compute a triangulation of only the blue vertices in linear time.