slides
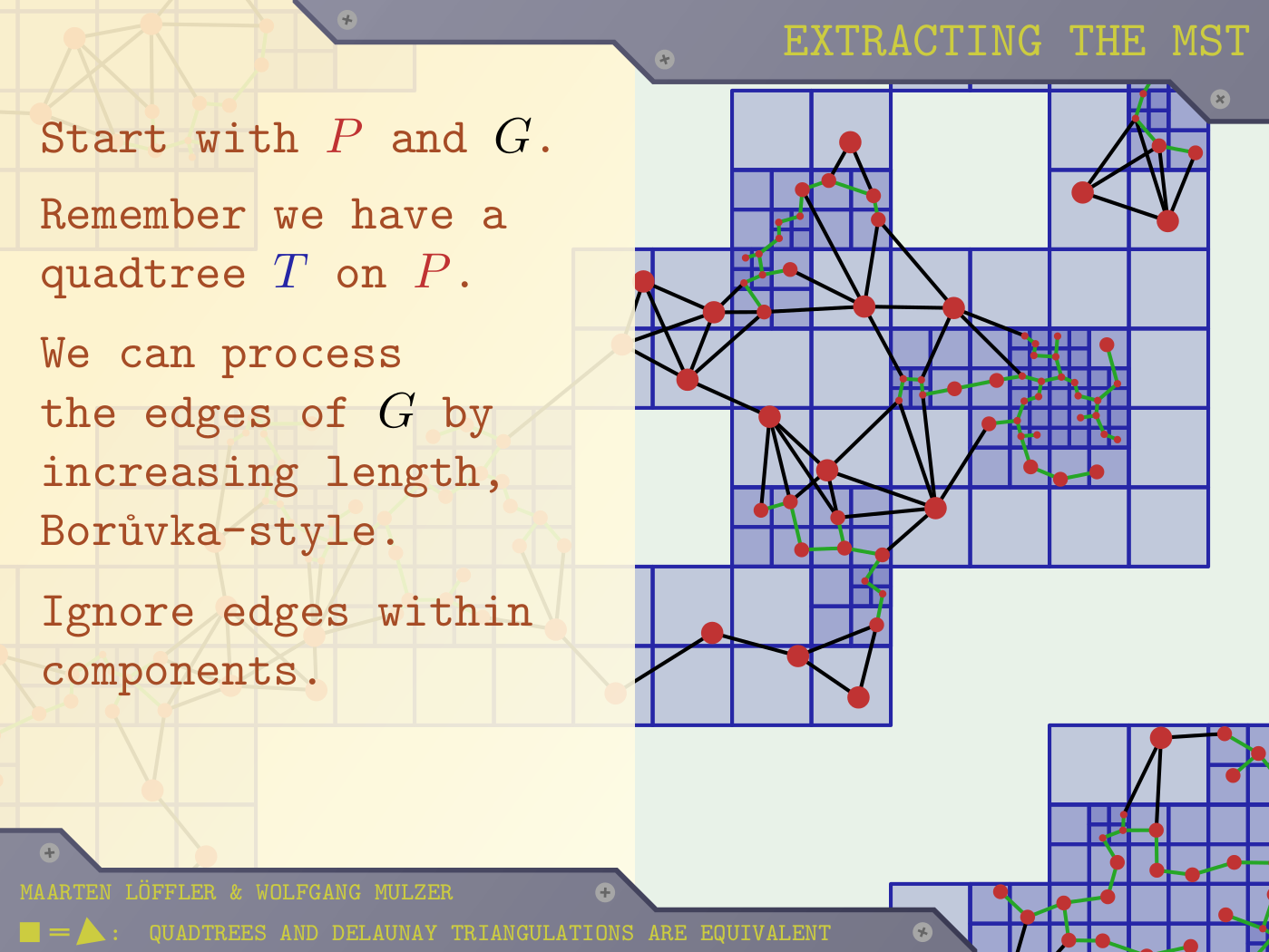
We show that Delaunay triangulations and compressed quadtrees are equivalent structures. More precisely, we give two algorithms: the first computes a compressed quadtree for a planar point set, given the Delaunay triangulation; the second finds the Delaunay triangulation, given a compressed quadtree. Both algorithms run in deterministic linear time on a pointer machine. Our work builds on and extends previous results by Krznaric and Levcopolous and Buchin and Mulzer. Our main tool for the second algorithm is the well-separated pair decomposition (WSPD), a structure that has been used previously to find Euclidean minimum spanning trees in higher dimensions. We show that knowing the WSPD (and a quadtree) suffices to compute a planar EMST in linear time. With the EMST at hand, we can find the Delaunay triangulation in linear time. As a corollary, we obtain deterministic versions of many previous algorithms related to Delaunay triangulations, such as splitting planar Delaunay triangulations, preprocessing imprecise points for faster Delaunay computation, and transdichotomous Delaunay triangulations.