Leo Maas
Ocean wave dynamics, Utrecht University

Welcome to my home page
| Employee information: | |
| Name: | Leo Maas |
| Department: | Ocean wave dynamics |
| Email: | l.r.m.maas@uu.nl |
| Telephone: | +31 30 253 3275 |
About:
Publications Students UU-course
|
Internal waves |
Tides
|
|
Ocean circulation |
Vortices |
|
Miscellaneous |
Wave attractors
Internal gravity waves in continuously stratified fluids |
|
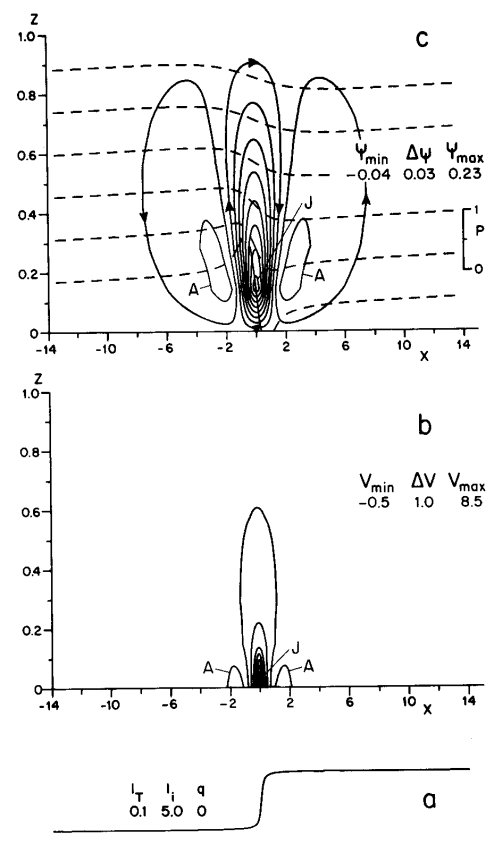
| A continuously stratified fluid supports internal gravity waves. These waves propagate obliquely through a fluid. Upon reflection they conserve their propagation angle with respect to the vertical. As a consequence, in a wedge, whose slope is less than that of the internal wave characteristics, waves get focused into the apex. During reflection from the sloping bottom they get focused and intensify. | 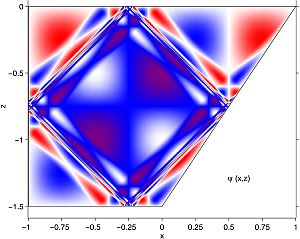 |
|
When one or more sidewalls of a container are steeper than the characteristics, these waves are focused or defocused upon reflection. In enclosed domains focusing dominates over defocusing, so that internal waves tend to be steered towards certain periodic orbits (wave attractors), where viscous and nonlinear effects act to absorb these. The following movie presents theory and some experimental results. Compare also the response of a tank having one sloping side wall to that in a tank with solely vertical and horizontal walls. Also see a side-view of a uniformly-stratified fluid, in which wave motion is visualized by means of fluorescent dye, injected in alternating horizontal layers, using a vertical laser sheet. The fluid has a sloping wall at the right, and the table on which the tank sits is oscillated vertically. By parametric excitation internal waves are generated : internal wave experiment. Subtracting the initially quiescent dye layers, the attractor is seen even better. Similar wave properties are found in inertial waves, arising in homogeneous rotating fluids. |
|
|
Links to related sites: Thierry Dauxois, Bruce Sutherland |
|
Field observations
| The internal tide in the Bay of Biscay is observed to constitute a beam whose structure is well-resolved with the help of a towed ADCP. A model predicts the beam to reflect from the bottom, and, depending on the presence and strength of a seasonal thermocline, to either reflect or scatter into a combination of thermocline waves and obliquely propagating internal waves. Observations deep down in the Bay of Biscay reveal "clean" spectra, with lots of mixed harmonics being generated by both tides and inertial oscillations. On the shelf observations show the thermocline "attracts" high shear due to inertial oscillations. |
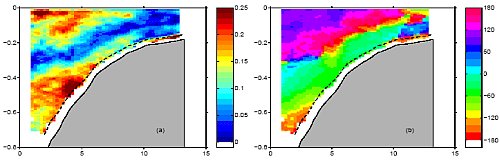
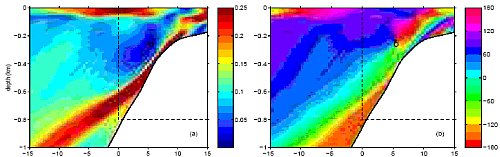
Internal tide amplitude (left; m/s) and phase (right, degrees) in vertical cross-sections obtained from Bay of Biscay field observations (top) and a numerical model (bottom).The observed area in the top panels corresponds to that inside the dashed rectangle in the bottom panels. Horizontal and vertical distances are given in kilometers (see Lam et al 2004, and Gerkema et al 2004) |
|
Observations reveal a geostrophic flow associated with a frontal region in the North Sea. Tidal advection of such a front may result in observed signals that might superficially be interpreted as free internal waves. When the sea is shallow, such as over shallow continental shelves, wind and tides mix the whole water column. At the edge of this, a shelf edge frontal region often exists, consisting of a bottom-to-surface front, which bounds an adjacent, oceanic water mass. This front behaves like a clamped string, and permits internal tides as standing waves.
|
Dead-water
|
Dead-water is a nautical term referring to a drastic decrease of a ship’s speed compared to its normal speed that arises when traversing through water that is density-stratified. The decrease in speed was reported to be up to a factor 5, giving the ship the appearance of having been brought to a full stop. The fluid can be stratified vertically due to variations in temperature or salinity. The decrease in speed is due to the fact that the ship is generating internal gravity waves on the interface between two layers. This process of wave generation is, unwantingly, very efficient when the ship has a draught comparable to the depth of the upper layer and when energy intended for propulsion is lost to internal wave generation. This process has been carefully studied and explained by V.W. Ekman (1904), following earlier observations on the Barentsz Sea by F. Nansen. |
||
|
An example of the dead-water phenomenon is given in the accompanying movie. It shows six successive experiments, performed in identical circumstances in a two-meter long tank filled with a dyed fresh water layer, and a thicker, salt-stratified lower layer. A little boat is dragged across the channel by means of a small weight of a few grammes, attached to a tiny wire, that is guided with the aid of two paperclips. There is a remarkable variation in the time needed to cross the channel depending on the nature of the interfacial gravity waves that are generated. |
Inertial waves in homogeneous rotating fluids
|
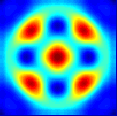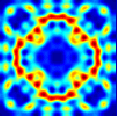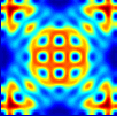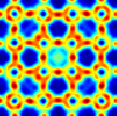
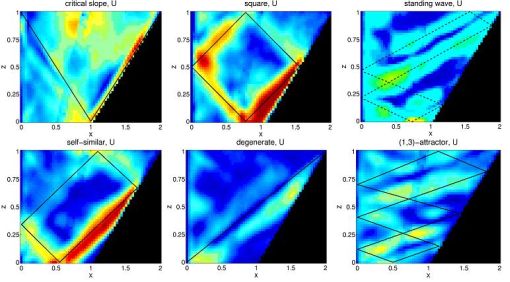
Homogeneous, rotating fluids support waves that are restored by the Coriolis force. These waves of frequency less than twice the rotation rate are similar to internal gravity waves in uniformly-stratified, non-rotating fluids in being also transverse, and in again being constrained in propagation direction, but now relative to the rotation axis. In particular, the waves will focus when reflecting from a sloping boundary onto wave attractors. However, because particle motion is circular instead of rectilinear, as for the internal gravity waves [which mathematically translates into a requirement that the pressure field satisfies oblique-derivative (Robin) boundary conditions], these waves generate spatially complicated patterns, even when just reflecting from vertical boundaries. See for instance the patterns of inertial wave energy distribution in a horizontal cube, shown in a plan view (horizontal mid-plane) in the left-hand corner of these web pages. Both stratified as well as rotating fluid systems (and also their oceanographically relevant combination) can accommodate waves of arbitrary frequency, thus denying the existence of eigenmodes. The spatial structure of these waves is determined by the Poincare equation, which is hyperbolic in spatial coordinates, and which is responsible for the unusual behaviour of these waves. See the spatial pattern of the observed current magnitudes (low/high presented as blue/red colors) and the redicted attractors (solid line) or standing mode (dashed line, upper right figure). These figures present side views taken from Astrid Manders" thesis, and the first reference below. |
||
|
A mean flow is generated above the location where the waves approach an attractor. In the lower/upper half of this frame the bottom is flat/ sloping upwards. It displays a steady, cyclonic dye displacement, presumably driven by the inertial waves that are forced by the modulation of the rotation (which itself is responsible for the observed periodic part of the motion). The inertial waves are geometrically focused by the sloping bottom. The mean flow that results from the angular momentum mixing that ensues is particularly strong over the middle part of the sloping region (3/4 upwards from the lower boundary of this frame) where the theoretical attractor reflects from the slope (and focusing occurs). |
||
|
Links to related sites: Joel Sommeria at rotating lab Coriolis/LEGI, Grenoble, |
|
|
-
Tides
Current observations
|
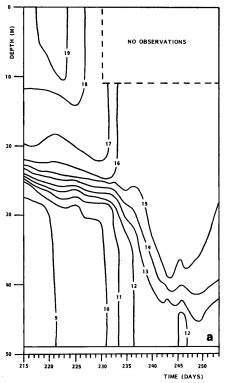
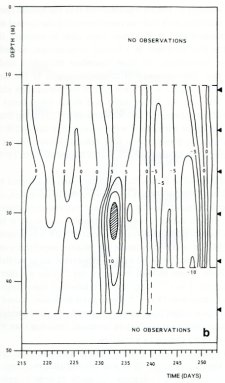
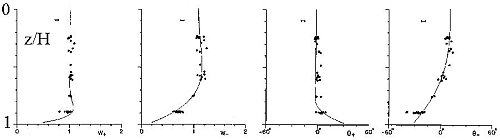
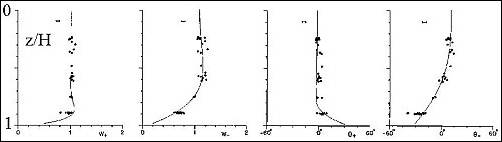
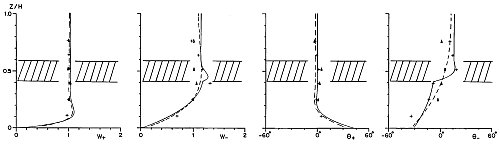
Observations of (oscillatory) tidal currents reveal the coexistence of two counterrotating Ekman layers. Only the thicker (anticyclonic) one affects the shear over a thermocline further up from the bottom. Lagrangian (drifter) compared to Eulerian (moored) current measurements reveal an increase of velocity gradients upon a decrease in separation scale. Here are observed amplitude W±and phase q± of the anticlockwise, or cyclonic (+) and clockwise, or anticyclonic (-) current components as a function of depth z, divided by water depth H. In the presence of a stratified thermocline the transfer of only the thicker anticyclonic current component is affected. |
|
|
|
Coastal resonance
|
Tides: Coastal resonance |
||
|
Coastal tides may either be choked (as in Lagoon type estuaries) or resonantly amplified. These two, contrasting type of responses might actually coexist as two stable equilibria when the resonance horn (ratio of reesponse over forcing amplitude versus frequency) is bent ove. This happens due to nonlinear effects (such as simply due to a sloping bottom). In that case, an irregular response may result when a perturbation is kicking the response from one to the other equilibrium and back. |
||
|
Links to related sites: Arjen Doelman |
|
|
Topographic filtering
|
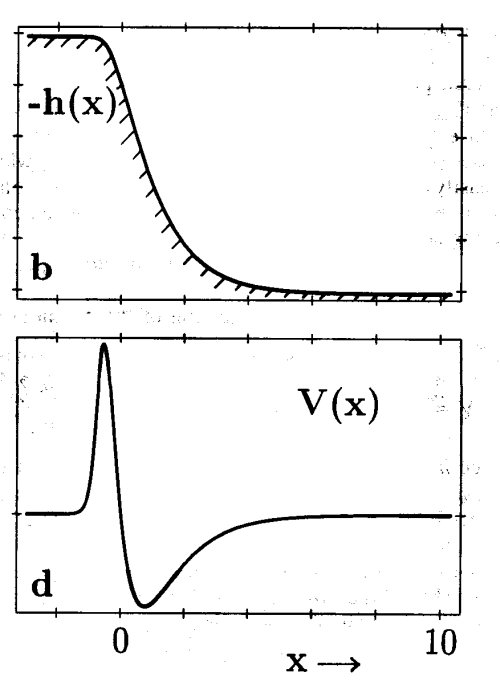
A topographic irregularity (particularly a continental shelf or ocean ridge) may act as a spectral (often low-pass) filter for incident long waves, which is evident through its presence in the potential of a Schrödinger equation. For some circumstances, however, the potential is reflectionless, and the shelf region behind a slope becomes vulnerable to incident long waves satisfying the corresponding criteria. |
|
|
For a typical shelf-slope topography (upper pannel) the localized nature of the scattering potential of the Schrödinger equation into which the problem can be cast is shown below. |
Rectified flows
|
Internal tides are both generated as well as advected by barotropic tides. The combined process acts to generate not only overtides, but also a mean flow. In a homogeneous sea, this barotropic, tidally-rectified flow extends over at most two tidal excursions beyond the slope in bottom topography. In the Northern Hemisphere it is directed such that it has the shallow side at its right-hand side. Stratification suppresses the vorticity stretching mechanism, responsible for the rectification, further away from the bottom. Apart from a frictional reduction close to the sea bed, this thus predicts a bottom enhancement of the tidally rectified flow. |
|
|
|
Publications:
-
 Aguiar-González, B.; Ponsoni, L.; Ridderinkhof, H.; van Aken, H.M; de Ruijter, W.P.M.; Maas, L (2016). Seasonal variation of the South Indian tropical gyre. Deep-Sea Res., Part 1, Oceanogr. Res. Pap. 110: 123–140. dx.doi.org/10.1016/j.dsr.2016.02.004 link to complete reference
Aguiar-González, B.; Ponsoni, L.; Ridderinkhof, H.; van Aken, H.M; de Ruijter, W.P.M.; Maas, L (2016). Seasonal variation of the South Indian tropical gyre. Deep-Sea Res., Part 1, Oceanogr. Res. Pap. 110: 123–140. dx.doi.org/10.1016/j.dsr.2016.02.004 link to complete reference
-
 de Fouw, J.; van der Heide, T.; Oudman, T.; Maas, L.R.M.; Piersma, T.; van Gils, J.A. (2016). Structurally complex sea grass obstructs the sixth sense of a specialized avian molluscivore. Anim. Behav. 115: 55-67. dx.doi.org/10.1016/j.anbehav.2016.02.017 link to complete reference
de Fouw, J.; van der Heide, T.; Oudman, T.; Maas, L.R.M.; Piersma, T.; van Gils, J.A. (2016). Structurally complex sea grass obstructs the sixth sense of a specialized avian molluscivore. Anim. Behav. 115: 55-67. dx.doi.org/10.1016/j.anbehav.2016.02.017 link to complete reference
-
 Ponsoni, L.; Aguiar-González, B.; Ridderinkhof, H.; Maas, L. (2016).
The East Madagascar Current: Volume Transport and Variability Based on Long-Term Observations. J. Phys. Oceanogr. 46: 1045-1065. dx.doi.org/10.1175/JPO-D-15-0154.1 link to complete reference
Ponsoni, L.; Aguiar-González, B.; Ridderinkhof, H.; Maas, L. (2016).
The East Madagascar Current: Volume Transport and Variability Based on Long-Term Observations. J. Phys. Oceanogr. 46: 1045-1065. dx.doi.org/10.1175/JPO-D-15-0154.1 link to complete reference
-
 Yu, J.; Maas, L.R.M. (2016). Linear waves in two-layer fluids over periodic bottoms. J. Fluid Mech. 794: 700-718. dx.doi.org/10.1017/jfm.2016.198 link to complete reference
Yu, J.; Maas, L.R.M. (2016). Linear waves in two-layer fluids over periodic bottoms. J. Fluid Mech. 794: 700-718. dx.doi.org/10.1017/jfm.2016.198 link to complete reference
-
 de Vries, J.J.; Ridderinkhof, H.; Maas, L.R.M.; van Aken, H.M. (2015). Intra- and inter-tidal variability of the vertical current structure in the Marsdiep basin. Cont. Shelf Res. 93: 39–57. dx.doi.org/10.1016/j.csr.2014.12.002 link to complete reference
de Vries, J.J.; Ridderinkhof, H.; Maas, L.R.M.; van Aken, H.M. (2015). Intra- and inter-tidal variability of the vertical current structure in the Marsdiep basin. Cont. Shelf Res. 93: 39–57. dx.doi.org/10.1016/j.csr.2014.12.002 link to complete reference
-
 Ponsoni, L.; Aguiar-Gonzáles, B.; Nauw, J.; Ridderinkhof, H.; Maas, L.R.M. (2015). First observational evidence of a North Madagascar Undercurrent. Dyn. Atmos. Oceans 72: 12-20. dx.doi.org/10.1016/j.dynatmoce.2015.08.002 link to complete reference
Ponsoni, L.; Aguiar-Gonzáles, B.; Nauw, J.; Ridderinkhof, H.; Maas, L.R.M. (2015). First observational evidence of a North Madagascar Undercurrent. Dyn. Atmos. Oceans 72: 12-20. dx.doi.org/10.1016/j.dynatmoce.2015.08.002 link to complete reference
-
 Ponsoni, L.; Aguiar-Gonzáles, B.; Maas, L.R.M.; van Aken, H.M.; Ridderinkhof, H. (2015). Long-term observations of the East Madagascar Undercurrent. Deep-Sea Res., Part 1, Oceanogr. Res. Pap. 100: 64-78. dx.doi.org/10.1016/j.dsr.2015.02.004 link to complete reference
Ponsoni, L.; Aguiar-Gonzáles, B.; Maas, L.R.M.; van Aken, H.M.; Ridderinkhof, H. (2015). Long-term observations of the East Madagascar Undercurrent. Deep-Sea Res., Part 1, Oceanogr. Res. Pap. 100: 64-78. dx.doi.org/10.1016/j.dsr.2015.02.004 link to complete reference
-
 Weijer, W.; Maltrud, M.E.; Homoky, W.B.; Polzin, K.L.; Maas, L.R.M. (2015). Eddy-driven sediment transport in the Argentine Basin: Is the height of the Zapiola Rise hydrodynamically controlled? J. Geophys. Res. Oceans; 120(3): 10.1002/2014JC010573. dx.doi.org/10.1002/2014JC010573 link to complete reference
Weijer, W.; Maltrud, M.E.; Homoky, W.B.; Polzin, K.L.; Maas, L.R.M. (2015). Eddy-driven sediment transport in the Argentine Basin: Is the height of the Zapiola Rise hydrodynamically controlled? J. Geophys. Res. Oceans; 120(3): 10.1002/2014JC010573. dx.doi.org/10.1002/2014JC010573 link to complete reference
-
 Gerringa, L.J.A.; Rijkenberg, M.J.A.; Thuróczy, C.-E.; Maas, L.R.M. (2014). A critical look at the calculation of the binding characteristics and concentration of iron complexing ligands in seawater with suggested improvements. Environ. Chem. 11(2): 114-136. dx.doi.org/10.1071/EN13072 link to complete reference
Gerringa, L.J.A.; Rijkenberg, M.J.A.; Thuróczy, C.-E.; Maas, L.R.M. (2014). A critical look at the calculation of the binding characteristics and concentration of iron complexing ligands in seawater with suggested improvements. Environ. Chem. 11(2): 114-136. dx.doi.org/10.1071/EN13072 link to complete reference
- Maas, L.R.M. (2014). Golven in de diepzee. Cah. Bio.- Wet. Maatsch. kwartaal 2: 28-33 link to complete reference
-
 Rabitti, A.; Maas, L.R.M. (2014). Inertial wave rays in rotating spherical fluid domains. J. Fluid Mech. 758: 621- 654. dx.doi.org/10.1017/jfm.2014.551 link to complete reference
Rabitti, A.; Maas, L.R.M. (2014). Inertial wave rays in rotating spherical fluid domains. J. Fluid Mech. 758: 621- 654. dx.doi.org/10.1017/jfm.2014.551 link to complete reference
-
 Bajars, J.; Frank, J.; Maas, L.R.M. (2013). On the appearance of internal wave attractors due to an initial or parametrically excited disturbance. J. Fluid Mech. 714: 283-311. dx.doi.org/10.1017/jfm.2012.479 link to complete reference
Bajars, J.; Frank, J.; Maas, L.R.M. (2013). On the appearance of internal wave attractors due to an initial or parametrically excited disturbance. J. Fluid Mech. 714: 283-311. dx.doi.org/10.1017/jfm.2012.479 link to complete reference
-
 Gerkema, T.; Maas, L.R.M.; van Haren, H. (2013). A Note on the Role of Mean Flows in Doppler-Shifted Frequencies. J. Phys. Oceanogr. 43(2): 432-441. dx.doi.org/10.1175/JPO-D-12-090.1 link to complete reference
Gerkema, T.; Maas, L.R.M.; van Haren, H. (2013). A Note on the Role of Mean Flows in Doppler-Shifted Frequencies. J. Phys. Oceanogr. 43(2): 432-441. dx.doi.org/10.1175/JPO-D-12-090.1 link to complete reference
- Gerkema, T.; Maas, L. (2013). Wiskundige aspecten van interne golven. Nieuw Arch. Wisk. 5/14(3): 172-176 link to complete reference
-
 Nurijanyan, S.; Bokhove, O.; Maas, L.R.M. (2013). A new semi-analytical solution for inertial waves in a rectangular parallelepiped. Phys. Fluids 25(2): 126601. dx.doi.org/10.1063/1.4837576 link to complete reference
Nurijanyan, S.; Bokhove, O.; Maas, L.R.M. (2013). A new semi-analytical solution for inertial waves in a rectangular parallelepiped. Phys. Fluids 25(2): 126601. dx.doi.org/10.1063/1.4837576 link to complete reference
-
 Rabitti, A.; Maas, L.R.M. (2013). Meridional trapping and zonal propagation of inertial waves in a rotating fluid shell. J. Fluid Mech. 729: 445-470. hdl.handle.net/10.1017/jfm.2013.310 link to complete reference
Rabitti, A.; Maas, L.R.M. (2013). Meridional trapping and zonal propagation of inertial waves in a rotating fluid shell. J. Fluid Mech. 729: 445-470. hdl.handle.net/10.1017/jfm.2013.310 link to complete reference