The strong interaction
Particle physics searches for the fundamental constituents of matter. There is now a very successful Standard Model, which explains the most important fundamental particles and three of the four fundamental interactions in nature. (One of the last missing ingredients of the Standard Model, the Higgs particle, was just recently discovered in experiments at the LHC accelerator at CERN.) Atoms are made of nuclei and electrons, nuclei in turn consist of protons and neutrons, and inside protons and neutrons we find quarks. As far as we know now, these quarks are elementary, i.e. have no further substructure. They are bound together by gluons, the “messenger” particles responsible for the strong interaction.
Quarks have very interesting, unusual properties. First of all, their strong interaction is due to a new charge-like property, which is called “color”. This is because it comes in three versions, which show an analogy to the three basic ordinary colors, and these “color-charges” are also called “red”, “green”, and “blue”. Apparently, quarks, which are “colored”, cannot exist as single particles. Nature allows only combinations of colored particles, which combine to a color-neutral state. This way three quarks can combine to form a proton or a neutron. Other three-quark combination are possible, which make other baryons, and combinations of a quark and an antiquark (i.e. a color and an anti-color) can form a so-called meson. In fact, apart from the proton these particles (which we call hadrons) are generally unstable. So, effectively quarks are always confined in hadrons and cannot exist as free particles.
This is related to the fact that the strong interaction between quarks increases in strength, when one tries to pull them apart, ultimately requiring an infinitely large amount of energy to fully separate them. Part of the Standard Model is a theory of this strong interaction, called Quantum Chromodynamics (QCD), which works very well in cases where the interaction can be treated as a small perturbation. For these cases it predicts the increase of the coupling with increasing distance. However, when the coupling gets too strong, QCD becomes non-perturbative and can no longer be solved analytically. This non-perturbative regime is particularly interesting, as it describes the phenomenon of confinement. Even more, it is also the regime, where the strong interaction contributes to generate the mass of the proton. Quarks themselves have only a very small mass according to theory - this small current mass is generated by the Higgs field. However, counting the three constituent quarks, this mass makes up less than 1% of the physical mass of the proton. We believe that most of the mass is generate dynamically by the strong interaction with a mechanism called spontaneous chiral symmetry breaking. These interesting features of the strong interaction are, however, not fully understood due to their non-perturbative nature.
The quark-gluon plasma
QCD calculations for some special situations, e.g. equilibrium thermal systems, can be performed numerically, using a discretised version of the theory, lattice QCD . Lattice QCD shows the phenomena of confinement and of chiral symmetry breaking. It also predicts a modification of the properties of the strong interaction for high temperature.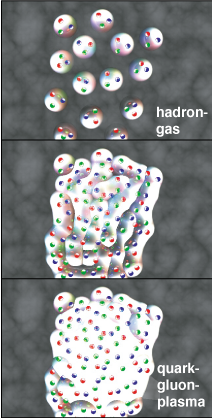 
Beyond some critical temperature, ordinary hadronic matter (as one finds e.g. inside a normal nucleus) should undergo a phase transition to a new state of matter, the quark-gluon plasma.This is illustrated in the figure on the left, which shows in the top panel a collection of independent hadrons each containing three quarks (a hadron gas, or also a model of a atomic nucleus). The quarks are confined inside the hadrons in so-called “bags” as illustrated by the white circles. The middle panel shows the state of such a system, when the density or equivalently the temperature has been increased up to the transition point, where the bags start to overlap. In the lower panel, all these bags have melted and formed a large volume of quark-gluon plasma. The confinement of quarks (and also gluons) in small volumes has disappeared, the matter is deconfined. The necessary temperature for this transition is of the order of 150-200 Megaelectronvolt (MeV, the "natural" temperature unit of high-energy physics), which corresponds to a few times 1012 K.