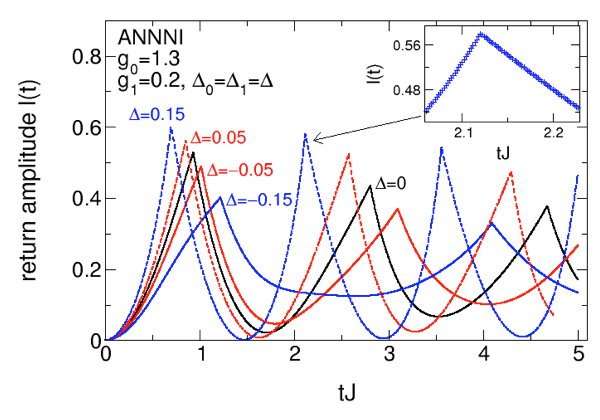
We have studied an implementation of Kitaev's toy model [A Yu Kitaev, Phys-Usp 44, 131 (2001)] for Majorana wires in an array of superconducting islands. We showed [1] that a capacitive coupling between the islands leads to an effective interaction between the Majorana modes. Using a Jordan-Wigner transformation we mapped the system to the ANNNI model and studied its phase diagram in detail (see Fig 1). We demonstrated that although strong repulsive interactions will eventually drive the system into a Mott insulating state, the competition between the band insulator and the Mott insulator leads to an interjacent topological state for arbitrary strong interactions. Indeed we were able [2,3] to show that the exact ground states can even be obtained analytically when the on-site (chemical) potential is tuned to a particular function of the other parameters. Using these exact ground states we demonstrated explicitly that there exists a set of operators each of which maps one of the ground states to the other with opposite fermionic parity. These operators can be thought of as an interacting generalisation of Majorana edge zero modes. Furthermore we have investigated [4] the interplay of interactions and disorder in the chemical potential. We found that moderate disorder or repulsive interactions individually stabilise the topological order, which also remains valid for their combined effect. However, both repulsive and attractive interactions lead to a suppression of the topological phase at strong disorder.
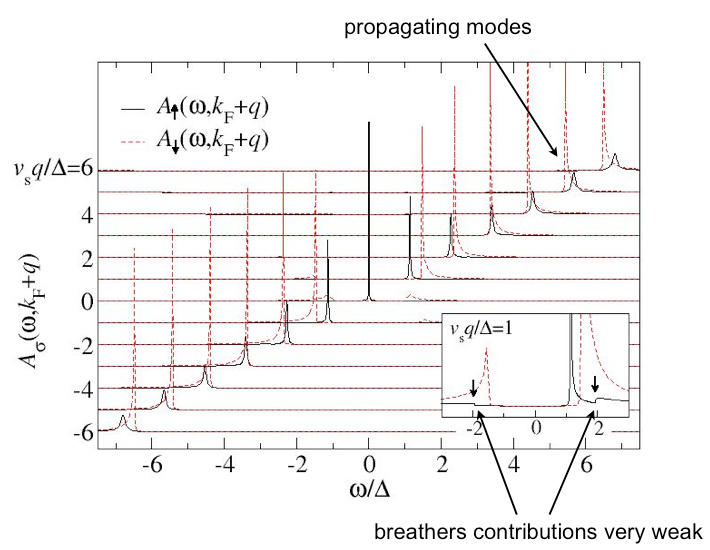
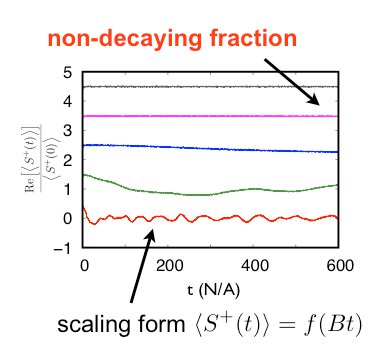
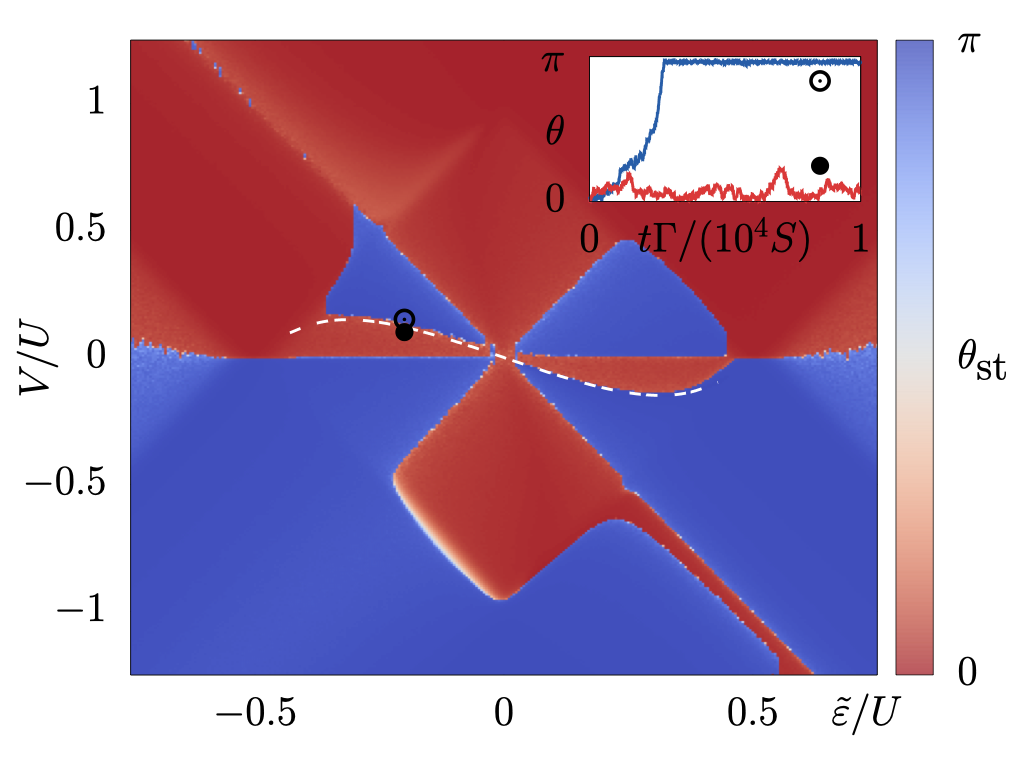
As a further project in the currently very active research field of topological insulators we have investigated the scattering off dilute magnetic impurities placed on their surface [5]. The interaction between the impurity moment and the electrons of the surface metal leads to mutual spin flips, such that backscattering could be allowed although time-reversal symmetry remains unbroken. Since the time-reversal symmetry remains intact the scattering off the magnetic impurity does not open new scattering channels in momentum space. Still the spin-flip processes lead to a distinct energy dependence of the quasiparticle interference (QPI) patterns as recorded by scanning tunneling spectroscopy. The most dramatic effect shows up at low energies where the Kondo effect occurs, ie, the impurity moments are screened by the surface-state electrons, despite their exotic locking of spin and momentum (see Fig 2).
[1] F Hassler and D Schuricht, New J Phys 14, 125018 (2012).
[2] H Katsura, D Schuricht and M Takahashi, Phys Rev B 92, 115137 (2015).
[2] J Wouters, H Katsura and D Schuricht, Phys Rev B 98, 155119 (2018).
[4] N M Gergs, L Fritz and D Schuricht, Phys Rev B 93, 075129 (2016).
[5] A Mitchell, D Schuricht, M Vojta and L Fritz, Phys Rev B 87, 075430 (2013).
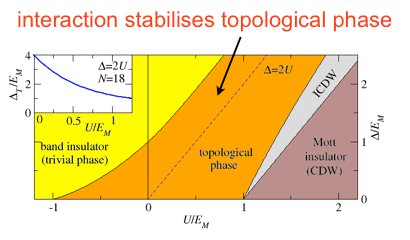
Fig 1: Phase diagram of the interacting Majorana chain [1]. Repulsive interactions facilitate the topological phase due to their competition with the on-site chemical potential. Inset: Gap along the blue dashed line.
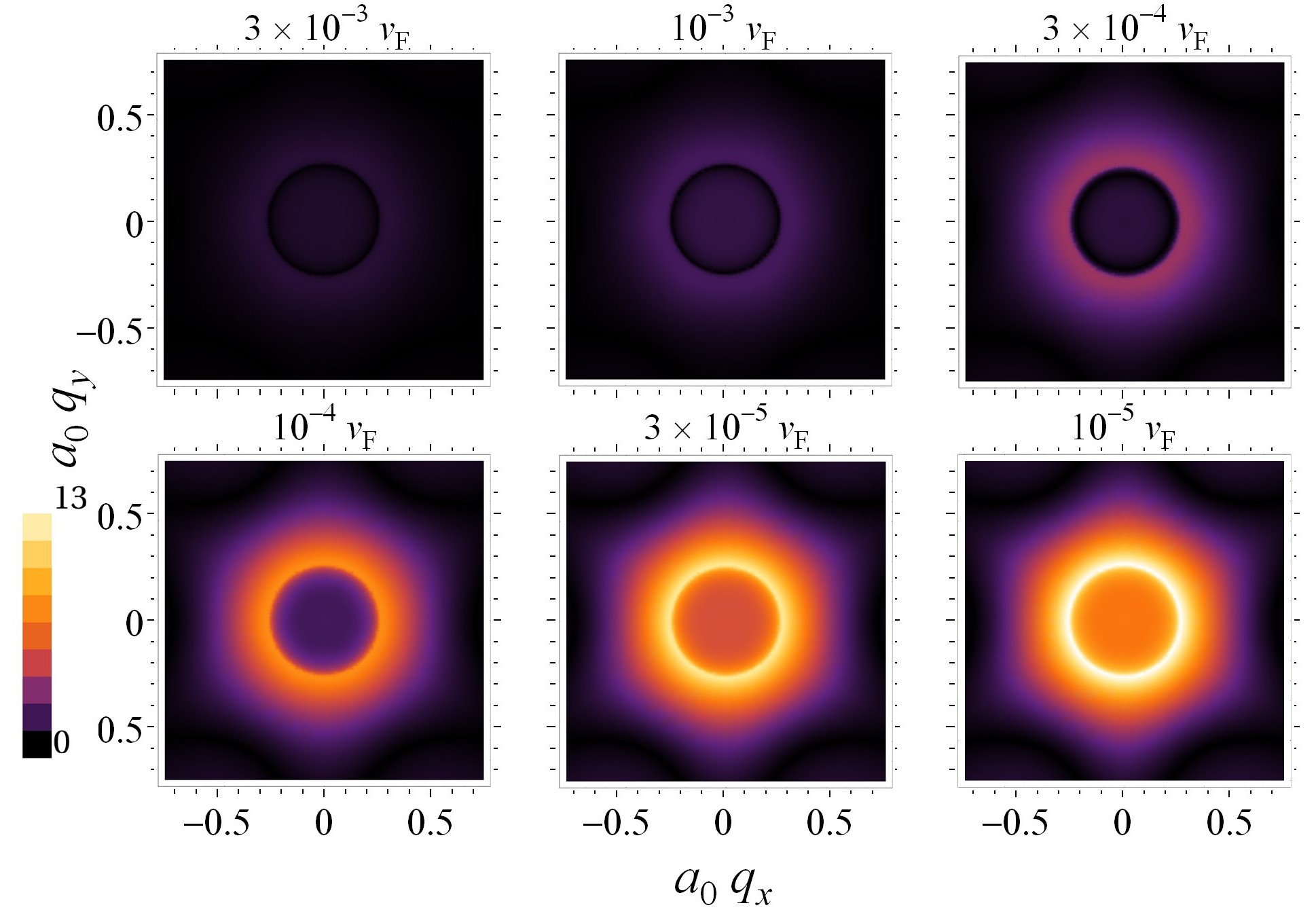
Fig 2: Quasiparticle interference patterns for a dynamic magnetic impurity [5]. At low energies there is a strong enhancement due to the Kondo effect.