A Een optelling, bijv 3+4, kan uitgevoerd worden met twee latjes, voorzien van de zelfde lineaire schaalverdeling: 4 optellen bij 3 betekent vanaf 3, 4 eenheden naar rechts opschuiven. Evenzo vindt men 7-4=3; vanaf 7 moet men 4 eenheden naar links opschuiven.
Vermenigvuldigingen en delingen kunnen op een dergelijke manier uitgevoerd worden, inden men beschikt over schaalverdelingen, waarbij een vermenigvuldiging 'omgezet' wordt in een optelling (en een deling in een aftrekking). Logaritmische schaalverdelingen bezitten deze eigenschap. (zie Rekenliniaal)
|
|
|
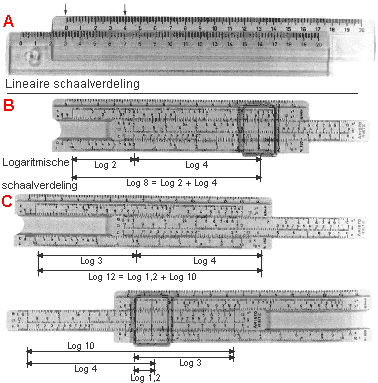
B Legt men twee logaritmische schalen nast elkaar en schuift men de 1 van de bovenste schaal boven de 2 van de onderste, dan leest men onder de 4 van de bovenste schaal af: 8=2 x 4. Een afstand log 4 naar rechts betekent vermenigvuldigen met 4. Een verschuiving over de zelfde afstand naar rechts, is dus delen door 4.
|
| C Op een rekenliniaalis een verdeling van 1 t/m 10 aangebracht. Wil men 3 x 4 met de rekenliniaal bereken, dan zal, wanneer de 1 boven de 3 geplaatst wordt, er geen antwoord afgelezen kunnen worden: de 4 valt buiten de onderste schaalverdeling. De bovenste schaal wordt dan naar links geschoven en de 10 boven de 3 geplaatst (er wordt door 10 gedeeld).Onder de 4 leest men dan af: 1,2. Het produkt van 3 en 4 is dus 1,2 x 10. Voor delingen geldt een overeenkomstige regel. Berekeningen als 3 x 4,7; 30 x 47 en 300 x 47 geven op de rekenliniaal allen de uitkomst 1,41. Tijdens de berekeningen moet dus steeds de orde van grootte van de uitkomst in de gaten gehouden worden.
|
|

