MAQ11306 exercises - Methyl-Chloroform

Goal:

Simulate the 1978-1993 concentrations of methyl-chloroform. Estimate the reaction constant between OH and methyl-chloroform. Determine how well methyl-chloroform constrains the OH level in the atmosphere. Discuss model uncertainties.

Introduction

The oxidizing capacity of the atmosphere is for a large part determined by the OH radical. This radical is produced as a result of ozone photolysis in the presence of water vapor:

O3 + hv ----> O(1D) + O2

O(1D) + H2O ----> 2 OH

On a global scale the most important sink for OH is its reaction with either CO or methane, relatively well mixed gases that limit the lifetime of OH to 1-10 seconds. In the planetary boundary layer, however, non-methane hydrocarbons may form the dominant OH sink, in particular in polluted and forested areas.

The lifetime of many trace gases, and most notably those of methane and CO, is determined by the reaction with OH. In order to understand the tropospheric trends and concentrations of these gases, knowledge of the tropospheric OH distribution and its temporal variation is of vital importance.

Methods to measure OH in-situ in the troposphere are rapidly being developed and these measurements show that the OH concentration is highly variable in space and time. This is expected on a theoretical basis, since the OH production is mainly determined by ozone, water vapor, and UV-B radiation, which are extremely variable in the troposphere. For instance, the variability of UV-B is caused by the variable solar zenith angle, clouds, surface reflections, and the overhead ozone column.

Since reaction with OH is the most important sink for methane, measurements of methane may be used to estimate the globally averaged OH concentration. This requires detailed knowledge of the methane sources. However, since methane is emitted by many anthropogenic and natural sources, estimates of the total source are rather uncertain.

Methylchloroform (1,1,1 trichloroethane, CH3CCl3, hereafter called MCF) provides a better opportunity to constrain tropospheric OH concentrations. Sources of this compound are purely anthropogenic and it is claimed that the emissions are known with high accuracy. Most sources are located in the northern hemisphere which results in a latitudinal gradient from north to south. Since the beginning of the 1990s the MCF concentrations in the troposphere are declining.

In global three-dimensional tropospheric chemistry modeling it has become a common exercise to test the calculated OH fields by simulating the MCF concentration at the so-called ALE/GAGE stations. Due to the uncertainties in the OH chemistry, rate constants, photolysis frequencies and the distribution of OH precursors and sinks, the accuracy of the calculated OH fields is limited. Therefore, some deviation between the measurements and the model results can be expected. It is estimated that a typical value of global mean OH is uncertain up-to about 25% due to kinetics imprecision.

In this exercise it will be investigated:

The loss rate is given by the product of OH and a reaction constant k. This reaction constant is temperature dependent and is given by:

  • k = ??? exp(--1550/T) cm3molecules-1s-1, with ??? to be determined and T in Kelvin.
  • 1x10-12 < ??? < 1x10-11 cm3molecules-1s-1

    • Remember that estimation of ??? is equivalent to an estimation of OH.

    • How consistent is the derived removal rate over longer periods?

    Exercise 7: Determine the rate constant for MCF + OH

    ALE/GAGE measurements of MCF have been taken from 1978. Five measurement stations are located in the 'clean' remote regions. Whenever applicable, pollution events have been omitted from the data. The asterisks in the following plots denote monthly averages. Bars denote standard deviations. It can be observed that the NH stations show considerably more variability due to the proximity of the sources. In the tropics, variability is mainly caused by convection.

    Mace Head (53N, 11W)

    Oregon (45N, 124W)

    Barbados (13N, 59W)

    Samoa (14S, 171W)

    Tasmania (41S, 145E)

    In order to simulate the MCF concentrations, we need to run the model for a longer period. The lifetime of MCF is 4-5 years, so we need a spin up time of at least 4 years. The model is initialized by concentrations of 40 ppt (parts per trillion) in 1975 and is run from then. First we set the reaction rate to

    • k = 5e-12*exp(-1550/T) cm3molecules-1s-1

    to see if this is a reasonable choice. The input file mcf.in requests a five year MOGUNTIA run and specifies the emissions (see EMISSION DISTRIBUTION) and chemical destruction by OH with the rate stated before.


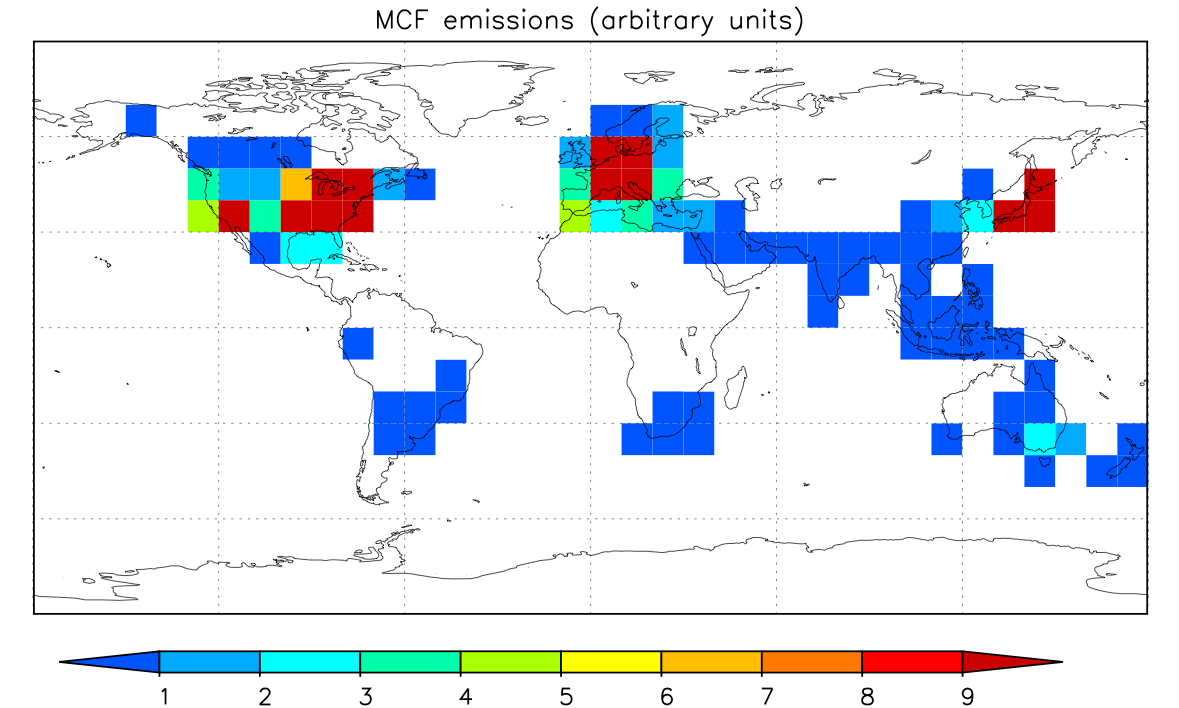
    Figure 1: MCF emission distribution.

    • run MOGUNTIA with the input file mcf.in (about fourty seconds)
    • Discuss the simulated seasonal cycle.
    • Discuss the latitudinal gradient.
    • Should the rate be higher/lower?

    Now, adjust the MCF + OH reaction rate and rerun:

    • Adjust the rate in mcf.in
    • Rerun MOGUNTIA up to 1980
    • Again, check the 1980 concentrations.
    • Check the seasonal cycle and the latitudinal gradient

    Once you are confident that the rate is about correct, a longer period can be simulated:

    • Adjust the END_DATE to 19940101 in mcf.in
    • Rerun MOGUNTIA up to 1994 (ignore the message at the end of the run by pressing <Enter>)
    • Compare simulation and measurements
    • Discuss differences in variability, seasonal cycle, and trend.
    • Estimate the uncertainty in the rate constant. This uncertainty can also be interpreted as uncertainty in the OH fields.
    • Is MCF a good tracer to constrain the OH fields (see introduction)?

    Exercise 8: More recent MCF measurements

    The simulation of MCF with MOGUNTIA seems to work reasonable for the period 1978-1994. A rigorous test for the estimated rate of removal (k OH) is the application of this removal to more recent measurements. Is the removal rate estimated for 1978-1994 applicable for 1990-2009? In this period, we are observing a decaying burden of MCF, due to strongly reduced emissions

    In order to set up a simualtion for the later period we need:

    • A suitable start concentration.
    • The optimized rate constant from the previous exercise.
    • Yearly emissions for the 1990-2009 period.
    • Measurements to check the consistency of the simulation.

    Measurements from the GAGE (red) and AGAGE (green) network can be found below.
    Mace Head (53N, 11W)

    Oregon (45N, 124W)

    Barbados (13N, 59W)

    Samoa (14S, 171W)

    Tasmania (41S, 145E)

    • Open the MOGUNTIA input file in an editor mcf_new.in.
    • Fill in the reaction rate that is consistent with previous exercise (1975-1993).
    • Estimate a suitable start concentration in 1990 from the plots above. Note that the concentrations in 1990 are much higher on the NH, some some compromise is needed.
    • Perform a simulation. Tip: to find a suitable start concentration, start with a run-time that is initially shorter (1990-1992).

    Questions

    • What do you observe for the seasonal cycle?
    • What do you observe for the north-south gradient in MCF?
    • How do these features compare to the observations?
    • How do the end concentrations match with the observed concentration?
    • What is your conclusion about the suitability of the rate constant derived for 1978-1994?
    • Did the global OH concentration change much from the 1980s to the recent period?

    Extra

    In reality we have to account for the uptake of MCF by the oceans and removal in the stratosphere. In this extra exercise we will investigate the impact of these additional sinks on the simulations

    • The time scale for removal by the ocean is estimated as about 80 years. The time scale for stratospheric removal as 45 years. Calculate the overall time scale for the combined processes
    • Select the LIFE_TIME such that the sink accounts for these removal processes
    • Redo the first exercise and re-estimate the removal rate (k).
    • Is this k lower or higher? Why?
    • Also repeat the second simulation, now with the newly estimated k and the estimated lifetime. Does the situation improve?