Assignment

Apart from the multiple-choice exam, the course is graded by an assignment. More details on how the assignment is to be completed is available here. Below the actual assignment is described.

Overview

The assignment consists of several successive steps. The context of the assignment is, briefly, as follows:

Construct an interactive application that implements several visualization techniques for a real-time simulation of fluid flow.

We provide the software source code of the real-time fluid flow simulation and a basic skeleton showing how to develop interactive visualizations atop of this simulation. A detailed description of the provided code is available here. Theoretical material supporting the assignment is provided during the lectures, in the lecture slides, and in the book. Practical support (questions, feedback on your intermediate results) is provided during the lab sessions by your instructor(s).

Above all, we encourage you to explore the assignment in different directions, and not to stay limited to the letter of this document. Visualization is much about designing creative solutions to the (given) problem of displaying complex data to gain different insights.

Structure

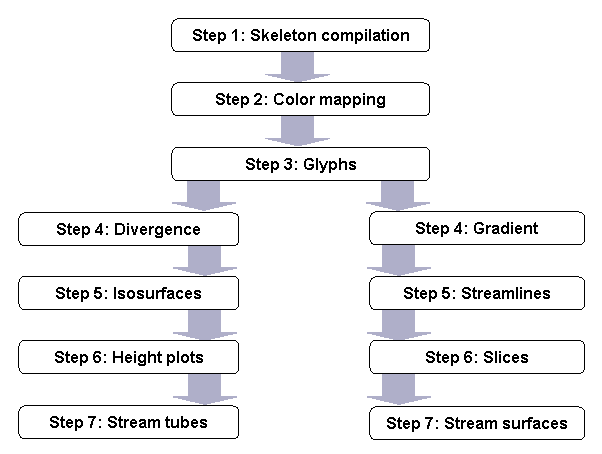
The assignment consists of several steps. To make things more challenging (and interesting), two variants of the assignment are offered. Steps 1-3 of both variants are identical. Steps 4-7 are different. The steps are ordered from simple to difficult, both in concepts and implementation. You have to choose and complete a single variant of steps 4-7. This is illustrated in the following diagram:

Step 1: Skeleton compilation

Aim:

The aim of this step is to get the skeleton application source code, provided by us, up and running. This involves getting the source code, performing the necessary adjustments to the build process and/or the source code to get it compiled, and finally getting the application running. This step is completed when you have obtained an interactive running application which shows the real-time fluid simulation; lets you control the simulation with the mouse; and displays the simulation graphically. Depending on your installed compiler and/or preferred programming languages, the amount of work needed to complete this step ranges between none to rewriting the entire skeleton code in your programming language of choice. More information is provided together with the skeleton code.

Book chapters:

none

Step 2: Color mapping

Aim:

The aim of this step is for you to design and implement a set of color mapping techniques for the fluid flow simulation. The color mapping techniques will be, during this step, applied to three datasets: The fluid density rho, the fluid velocity magnitude ||v||, and the force field magnitude ||f||. For a description of these quantities, see the skeleton code.

There is already a basic implementation of color mapping provided in the skeleton code. Using this implementation as a starting point, and also the material in the book and lectures, you have to implement yourself several new functionalities, as follows.

• Implement a mechanism that lets you choose between several colormaps. For each colormap, you should display a color legend, e.g. in the form of a colored bar, somewhere in the visualization’s user interface. Think of something similar to figure 5.6 in the book as a starting point. The legend should show both the colormap and the corresponding numerical values associated to various colors. Atop of this mechanism, implement at least three different colormaps:
  • a rainbow, or blue-to-red colormap (see Fig. 5.2 a)
  • a grayscale, or black-to-white colormap (see Fig. 5.2 b)
  • another colormap of your own choice, e.g. a red-to-white, or blue-to-yellow, or similar colormap.
• Implement a mechanism that lets you parameterize the colormap itself. There are several values you can think of tuning for a given colormap:
  • the number of actual colors used in the colormap. A good range is 2..256 different colors. See Figure 5.6.
  • the saturation and hue of the actual colors. See Section 3.6.3 (Color attributes)
• Implement a mechanism that lets you choose how you want to apply the colormap on the actual dataset. Two options should be supported:
  • scaling: the entire actual range (min..max) of the dataset at the current time moment is mapped to the visible colormap. This means, of course, that you have to update the numerical values displayed along with the color legend.
  • clamping: the data values are clamped between two user-prescribed min and max values. These values correspond to the entire range of your color legend. Actual data values higher than min, or lower than max, are actually clamped to min and max respectively. The user should be allowed to change min and max interactively, e.g. by means of some sliders or similar widgets.

Since there are several datasets you should apply the color mapping on, you should provide some means in the visualization to choose the dataset (rho, ||v||, or ||f||) you want to visualize. The dataset rho is readily available in the skeleton code. However, for the other two, you may need to compute them on the fly.

Book chapters:

Chapter 5, section 5.1 (Color mapping)

Step 3: Glyphs

Aim:

The aim of this step is to design and implement a set of glyph techniques. Glyphs are icons that convey the value (orientation, magnitude) of a vector field by means of graphical icons, such as arrows. Glyphs can also be used to visualize several fields together, such as one scalar field and one vector field, at the same spatial locations. You will design and implement several glyphs to visualize three datasets: The fluid density rho, the fluid velocity v, and the force field f. For a description of these quantities, see the skeleton code.

The skeleton code already contains a basic implementation of hedgehog glyphs. Using this as a starting point, and also the material in the book and lectures, implement several new functionalities, as follows.

• Implement a mechanism that lets you choose one scalar field and one vector field and visualizes their combination using glyphs. As scalar fields, you should be able to choose from: the density rho, the fluid velocity magnitude ||v||, and the force field magnitude ||f||. These are the scalar fields used at step 2. As vector fields, you should be able to choose from: fluid velocity v and the force field f. Use the vector field direction and magnitude to control the orientation and length (respectively) of the arrows. Use the scalar field to control the arrows’ colors. For this, use the color map techniques designed at step 2.
• Implement a mechanism to specify where to draw the glyphs. Start by modifying the mechanism currently implemented in the code which places the glyphs on a regular sampling of the grid. Provide interactive controls to specify the number of samples, in the x and y directions, where you want to display the glyphs. If your sample points do not coincide with an actual grid point, provide interpolation mechanisms that compute the data values out of the grid neighbour point(s). Here, you can choose between nearest-neighbor (constant) and (bi)linear interpolation.
• Implement a mechanism that lets you parameterize the glyph itself. Besides using simple two-dimensional arrows (hedgehogs), implement two other glyph types that are able to show both a vector field and a scalar field. Suggestions include, but are not limited to:
  • three-dimensional cones
  • three-dimensional ellipsoids
  • three-dimensional arrows consisting of a cone tip and a cylindrical shafts
  • arrows implemented as two-dimensional nice-looking, high-quality, textures instead of simple polygonal shapes

Provide interactive means to choose the datasets and types of glyphs at runtime. Consider carefully the glyph design: How thick to make the glyph? How long to make it? Should you scale the length linearly with the vector magnitude, or use another scale? Should you clamp the glyph’s minimal and maximal sizes to some values? If so, which are those?

Book chapters:

Chapter 6 – Sections 6.2 (Vector Glyphs) and possibly 6.3 (Vector Color Coding)

From here on, the assignment branches.

Step 4a: Divergence

Aim:

The aim of this step is for you to understand and implement a set of vector field operators. Vector field operators are used to compute various quantities on vector fields, which enable different types of analyses to take place on the vector data. In this step, you will implement the computation of the divergence operator. Informally put: the divergence of a vector field v, denoted as div v, is a scalar quantity which shows, at every point, the amount of mass which is compressed or expanded while flowing in that field. A zero divergence value means the field neither compresses nor expands mass. If mass enters the field at some point, called a source point, then that point has a positive divergence value. If mass exits the field at some point, called a sink point, then that point has a negative divergence value.

In this step, you have to implement the following:

• Compute the divergence div v of the fluid velocity field v. This delivers a scalar field, sampled on the same grid as the velocity field. Next, visualize the divergence field, using the color mapping implemented in step 2.
• Do the same as above, now for the force field f. What relation do you see between the divergence div f and the force field magnitude ||f|| itself?

Hints: Start from the divergence definition. Compute the partial derivatives in this definition directly from the discrete data available on the simulation’s grid. For this, see Chapter 3 – Section 3.7.

Book chapters:

Chapter 6 – Section 6.1 (Divergence and Vorticity) and Chapter 3 – Section 3.7 (Computing Derivatives of Sampled Data)

Step 4b: Gradient

Aim:

The aim of this step is for you to understand and implement a set of scalar field operators. Scalar field operators are used to compute various quantities on scalar fields, which enable different types of analyses to take place on the scalar data. In this step, you will implement the computation of the gradient operator. Informally put: the gradient of a scalar field s, denoted as grad s, is a vector quantity which shows, at every point, the direction in which s increases most at that point. The gradient length equals the amount of change per unit length in the direction of maximal variation, or, in other words, the derivative of the scalar quantity s in that direction. A zero gradient (zero length, undefined direction) signals a point around which the scalar quantity is constant.

In this step, you have to implement the following:

• Compute the gradient grad rho of the fluid density rho. Next, visualize the gradient field, using the glyph functionality implemented in step 3.
• Do the same as above, now for the fluid velocity magnitude ||v||. What relation do you see between the gradient grad ||v|| and the velocity field v itself?

Hints: Start from the gradient definition. Compute the partial derivatives in this definition directly from the discrete data available on the simulation’s grid. For this, see Chapter 3 – Section 3.7.

''Book chapters:

Chapter 2, page 28 (gradient definition), Chapter 3 – Section 3.7 (Computing Derivatives of Sampled Data), and possibly Chapter 9, p. 293 (gradient computation for images)

Step 5a: Isolines

Aim:

The aim of this step is for you to understand and implement the isolines technique. Isolines show all points of a scalar dataset’s domain where the scalar equals a given value (or values). You will have to implement the computation of isolines to visualize the fluid density rho. The easiest to proceed is to construct isolines in a cell-by-cell fashion. For every cell, compute the intersection of the isoline with the cell’s edges, and render the resulting line segment(s), if any. You can use the marching squares technique to accelerate the isoline-cell intersection, if desired. However, this is not a requirement – other implementations are allowed as well, as long as the isolines are computed and rendered in real-time, as the fluid dynamically changes.

In this step, you have to implement the following:

• Given a scalar value rho₀ for the fluid density, compute and render the isoline for that value over the grid. The value rho₀ should be interactively settable by the user. Consider the fact that the dataset’s range (minimum and maximum) for rho dynamically changes in time.
• Given two scalar values rho₁ and rho₂ for the fluid density, and an integer number n, compute and render n isolines equally distributed over the range [rho₁ ,rho₂]. As above, make rho₁ , rho₂ , and n settable by the user.
• Color the rendered isolines with their scalar value, using the already implemented colormap algorithms.

Book chapters:

Chapter 5, Section 5.3 – consider only the 2D (isolines) case.

Step 5b: Streamlines

Aim:

The aim of this step is to understand and implement the streamlines technique. Streamlines visualize trajectories of imaginary particles released in vector fields, starting from a given seed point. In this step, you will implement the computation of streamlines to visualize the fluid velocity field v. Proceed as follows:

• Given a starting point p in the domain of the vector field, construct the streamline by integrating the field v upwards. The simplest is to use Euler integration. Thus, given p, compute the following point p_next that a particle released at p would travel to in the field v by using p_next= p + v(p)*Dt, where v(p) is the value of v at p and Dt is a (small) time step. Render the streamline segment pp_next. Then, repeat the process by replacing p with p_next.
• Color the streamline using the velocity field magnitude ||v|| via the colormap technique already implemented.
• Consider how to set the values of the seed (start point p) and the time step Dt, and the streamline tracing stop-criterion:
  • Set the seed point p by clicking with the mouse on the dataset’s domain.
  • Set the time step Dt so that a streamline segment pp_next has always the same given length. This length should be a small fraction of the grid cell size, e.g. 0.25 up to 0.5. For this, you actually should normalize v(p) when tracing the streamline. Consult the indicated book chapters for details.
• Stop tracing the streamline when: either its total length exceeds some maximal length (e.g. 5 times the grid’s edge-size), or when it exits (leaves) the grid.
• Consider how to compute the vector field value v(p). As you notice, p can be at an arbitrary location, i.e. not necessary at a cell (grid point) vertex. The easiest is to determine the cell p falls within, and then to compute v(p) by linearly interpolating, at p, the values of v at the four cell vertices.

Book chapters:

Chapter 6, Section 6.5 – consider only streamlines.

Step 6a: Height plots

Aim:

The aim of this step is for you to understand and implement the height plot technique. Height plots are used to visualize scalar functions defined over (planar) 2D domains by plotting the function values along the third (z) dimension. In this step, you will implement the height plot technique, and use it to visualize the fluid density rho, the velocity magnitude ||v||, and the force magnitude ||f||. Proceed as follows:

• Implement the height plot algorithm atop of the simulation grid. Use the already existing simulation grid geometry as base plane for the height plot.

The plot will be hence drawn in 3D, atop (or below) of this plane. The input of the plot should be user settable, i.e. one of the scalar fields named above. Of course, the plot should dynamically change with the simulation.

• Since the height plot is a 3D structure, you have to implement appropriate shading and viewpoint selection mechanisms. In both cases, use only simple techniques, bearing in mind that this is a visualization, not a rendering, assignment. A Gouraud shaded plot, based on a Phong lighting model with fixed material parameters, a fixed white bi-directional light source placed above the scene and shining downwards, should be enough for lighting. For viewpoint selection, do not implement a full-fledged interactive viewpoint manipulation system, as this is quite complex. Provide just a simple mechanism that, for example, lets one turn the scene around the grid’s center, and possibly constrains the view directions to lie above the ground plane. Zooming mechanisms can also be quite limited. Think of ergonomics: the best viewpoint manipulation is done via the mouse, but it is more complex to implement. If you are unsure on how to do this, implement first a viewpoint manipulation based on classical GUI elements (e.g. sliders), after which you can go do the more challenging mouse-based manipulation
• Use the color of the plot to show a separate scalar field, via the already familiar color mapping technique. For example, the plot height can show rho, and the plot color can show ||f||

Book chapters:

Chapter 2, Section 2.2 (rendering basics) and Section 2.3 (rendering the height plot); Chapter 5, Section 5.4 (height plots)

Step 6b: Slices

Aim:

The aim of this step is for you to understand and implement the time-dependent slices technique. Slices are typically planar grids used to extract (and visualize) data from a higher-dimensional dataset, e.g. a cube. However, slices can be used for different purposes apart from extracting 2D planes from a 3D volume. In this step, you will use slices to visualize the time dimension of the flow simulation. Consider a 3D volumetric dataset formed by "stacking" along the z dimension the 2D planar grids g_i corresponding to the simulation steps at consecutive moments g_i. Think of a FIFO buffer, of some fixed given length, which receives the grids g_i containing the simulation results of consecutive time steps. This buffer is actually our 3D volume. We can use slices to visualize this volume, and explicitly show the actual time variation of data. Proceed as follows:

• Design and implement an infrastructure that takes any of the previously implemented planar visualization techniques (i.e. color-mapped planes, glyphs, and isolines), and draws n such visualizations, stacked atop of each other in the z direction. For this, design first a data structure to store the results of n time frames, and with a FIFO buffer behavior. A simple solution is to use a fixed array of n grids, indexed in a cyclical manner (also known sometimes as a "ring buffer"). After you implemented this structure, draw its n grids atop of each other, equally spaced along the z direction. The value n should be settable by the user, and allow for at least 20 frames (n>=20)
• The previous step will result in a set of opaque slices stacked atop of each other. You must provide a means to "see through" the data. For this, use the transparency (or alpha) channel of the rendered slices. Provide two controls here. First, let the user specify a global alpha value a_global. Second, modulate (i.e. multiply) this global value with a data-dependent value a_data, as follows. For glyphs, the data-dependent value adata should be a function of the velocity vector magnitude. For isolines, a_data should be a function of the isoline scalar value. For color-mapped planes, a_data should be a function of the scalar value. In all cases, use a function a_data(v) which produces a high opacity value (i.e. 1) for high data values v, and a low opacity value (i.e. 0) for low data values v. The exact shape of the function a_data is up to you.
• Since you design now a 3D visualization, you must add 3D viewing capabilities. For this, follow the instructions delivered at Step 6a, substep 2 (except the lighting, which is not needed).
• Since you use transparency, do not forget to enable alpha blending. Also, render the slices in back-to-front order, i.e. from the stack’s top (high z values) to the bottom (low z values). In other words, "recent" time frames enter from the stack's top, trickle down, and exit through the bottom.

Book chapters:

Chapter 2, Section 2.2 (rendering basics) and Section 2.5 (transparency basics); Chapter 10, Section 10.2 (volume visualization basics)

Step 7a: Stream tubes

Aim:

The aim of this step is to implement the stream tubes technique. Stream tubes are similar to streamlines. They display paths of particles in a typically 3D vector field as cylindrical tubes whose cross-section size can vary to encode additional parameters. To use this technique, we need a 3D vector field. We can obtain one from our 2D time-dependent simulation, if we consider time as the third (z) dimension. For this, proceed as in step 6b: Design a data structure that stores consecutive time frames from the simulation, with their corresponding data values. Aligning this slices along the time dimension gives you a 3D vector field. In this field, next, construct the stream tubes as follows:

• First, provide a mechanism to place (and remove) seed points in the 3D volume. The seed points themselves should be visible as small glyphs, e.g. colored spheres. Think of (and solve) the problems of 3D seed point placement. A simple solution is to allow the user to control the (x,y,z) position of a seed point by means of sliders. A more involved, though easier to use, way is to allow users to click in some point in the window. This delivers two coordinates. Adding a subsequent third (depth) coordinate value can be done via a slider, or even better, by mouse interaction such as mouse wheel or sliding the mouse in combination with control keys.
• After you have placed the seeds, trace streamlines from these seeds in the 3D vector field. For details on the streamline technique, see step 5b. Adapt these techniques as needed to accomodate three dimensions instead of two.
• For each traced streamline, construct a stream tube geometry around it. For this, first define what the cross-section of the tube should be. A good starting point is to use a square (four points). Next, use a circle sampled as a closed polyline with n points, where n is a parameter with values between 3 and 10. For each sample point p_i along a streamline, construct such a cross-section. The cross-section should be orthogonal to the current polyline segment p_ip_i+1. Finally, connect the corresponding points of all consecutive cross-sections to generate the stream tube geometry as a set of quadrilaterals.
• Several technical details are important. First, do not use a too high sampling resolution for the streamlines and/or the cross-sections. This can easily generate (tens of) thousands of polygons, which slows down the visualization. Second, how to exactly place the cross-section? It is relatively easy to design a rotation that moves the cross-section points, from a 2D reference coordinate system, so that the cross-section becomes normal to the local streamline segment, but how to rotate the cross-section then around the streamline itself? To do this, you need a full 3D reference frame, placed at each streamline point, which indicates the exact position and orientation of the cross-section. Several solutions are possible. A simple one is to consider a coordinate frame u,v,w where: u is tangent to the streamline segment p_ip_i+1; v is the cross-product of the two consecutive streamline segments p_i-1p_i

and p_ip_i+1; and w is the cross-product of u and v. This type of rotation should deliver a stream tube where the cross-section does not rotate too much around the streamline itself, but gets "swept" along it. Finally, consider the shading and coloring of the stream tubes: Use either flat or Gouraud shading, and either a constant color, different for each stream tube, or a color map which shows one of the scalar fields along the streamline, such as velocity vector magnitude ||v|| or density rho.

• Finally, consider the size (diameter) of the streamtubes. First, implement the above method using a constant diameter. Next, have stream tubes to use a variable diameter, which is linearly scaled to show one of the scalar field values in the simulation, such as velocity vector magnitude ||v|| or density rho. The choice of which field to display is up to you.

Book chapters:

Chapter 6, Section 6.5 - streamtubes and streamlines.

Step 7b: Stream surfaces

Aim:

The aim of this step is to implement one variation of the stream surface technique. Stream surfaces are generated by advecting a 1D curve in a 3D vector field, which creates a surface. This gives a spatial overview of the complexities of the flow in a more continuous, less disruptive, way than when using lower-dimensional primitives such as glyphs or streamlines. Proceed as follows:

• First, define the 1D curve primitive that you want to sweep to create the stream surface. A simple choice is to use a line (represented as a polyline). The placement of this curve in the 3D vector field is important, just as seeds are for streamlines: Placing the seed curve at a "wrong" location may generate a stream surface which is not very interesting. Design an interactive mechanism for placing the seed curve in the volume. For example, you can use interactive placing of its two endpoints, in a similar way as the stream tube seedpoint placement suggested for step 7a, and next sample the line between these endpoints to create your polyline. Consider all the interaction points indicated for step 7a.
• Next, create streamlines from every sample point generated on the seed curve in the previous step. Trace these streamlines "in parallel", that is, advance one step at a time along all streamlines. After one step, this should deliver you the next location of the stream curve. Connect the corresponding points along each two consecutive stream curves to obtain your stream surface.
• Several technical points are important here, as follows. First, control the streamline step size such that you advance at equal speed along all streamlines. If not, your stream surface can badly warp and self-intersect, creating a messy visualization. Second, carfefully tune the sampling density of the initial stream curve, so you do not generate too many, but also not too few, streamlines. Too few streamlines will create a non-smooth stream surface. Finally, consider what happens when one of the traced streamlines leaves the data volume, but the others can still advance. Here, you should keep tracing the remaining streamlines and construct the remainder of the surface in the volume, as long as possible.
• Finally, consider the coloring and shading of the stream surface. Since the surface is actually a quad mesh, you can compute vertex normals by the classical normal averaging technique, and use Gouraud (smooth) shading. Take care to use bidirectional lighting, instead of the simple unidirectional lighting, which may be the default your graphics library (OpenGL) uses. This is important as it enables users to see both faces of the stream surface. Finally, color the surface using color-mapping to show one of the scalar fields, such as the velocity magnitude ||v|| or the density rho. The choice of the actual scalar field is up to you.

Book chapters:

Chapter 6, Section 6.5 – study the entire section

Bonus Step (optional): Image-Based Flow Visualization

Aim:

This step delivers an extra point to anyone implementing it, independent on the previous steps. Both tracks (a) and (b) can choose to implement this step. This step is optional: Do it if you feel up to the challenge and/or want a higher grade, as the step is not mandatory. Also, note that this step is technically more involved than the previous ones.

The aim of this step is to implement the Image-Based Flow Visualization (IBFV) method presented during the lecture and described in the book (Chapter 6, Section 6.6). IBFV uses a set of techniques including two-dimensional texture warping, blending, and noise textures, to produce a dynamic animation of small black-and-white particles in the direction of the flow, in real-time. Your goal is to implement this method in order to visualize the velocity vector field v of the flow simulation. Proceed as follows:

• First, study the IBFV method and pseudocode from the book. Pay attention to the pseudocode, as there are a few subtle points there.
• Next, decide how easy is (and, if it is overall feasible) to integrate this method atop of your actual visualization infrastructure. In particular, to successfully implement this method, you need to have access to several graphics ingredients, such as: defining several high-resolution 2D textures; and being able to read color data back from the screen into the texture memory. While these steps are trivial to do in standard OpenGL, as shown by the pseudocode, this may not be the case, depending on the exact type of graphics API or toolkit that you are using.
• If all works fine at an implementation level, decide how to couple the simulation (time-dependent) vector data and the visualization. You can, for example, let the visualization read the simulation vector field every time when it changes, i.e. after every simulation step. You can also decide to let the visualization read a new "frame" of the simulation vector field data only after n visualization frames have been rendered, where n would be some user-defined constant, e.g. 20. The two approaches give different types of results – remember the discussion between streamlines and streaklines, for example.
• Finally, you should add an interactive means of controlling the blending factor, one of the most important parameters of this type of visualization, to your tool's interface.

Book chapters:

Chapter 6, Section 6.6 – texture-based vector visualization

Grading

All steps count equally towards the final grade. The bonus step (if completed successfully) gives an extra point. As such, the bonus step can be used to get the maximum (or a higher) grade if you do not want to complete all sub-steps of all previous steps.