Abstract

Path planning for walking characters in complicated virtual environments is a fundamental task in simulations and games. A navigation mesh is a data structure that allows efficient path planning. The Explicit Corridor Map (ECM) is a navigation mesh based on the medial axis. It enables path planning for disk-shaped characters of any radius.

In this paper, we formally extend the medial axis (and therefore the ECM) to 3D environments in which characters are constrained to walkable surfaces. Typical examples of such environments are multi-storey buildings, train stations, and sports stadiums. We give improved definitions of a walkable environment (WE: a description of walkable surfaces in 3D) and a multi-layered environment (MLE: a subdivision of a WE into connected layers). We define the medial axis of such environments based on projected distances on the ground plane. For an MLE with n boundary vertices and k connections, we show that the medial axis has size O(n), and we present an improved algorithm that constructs the medial axis in O(n log n log k) time.

The medial axis can be annotated with nearest-obstacle information to obtain the ECM navigation mesh. Our implementations show that the ECM can be computed efficiently for large 2D and multi-layered environments, and that it can be used to compute paths within milliseconds. This enables simulations of large virtual crowds of heterogeneous characters in real-time.

References

• Wouter G. van Toll, Atlas F. Cook IV, Marc J. van Kreveld and Roland Geraerts. The Medial Axis of a Multi-Layered Environment and its Application as a Navigation Mesh. ACM Transactions on Spatial Algorithms and Systems. Vol. 4, No 1. pages 2:1-2:34. May 2018.

  

  

• Wouter G. van Toll, Atlas F. Cook IV and Roland Geraerts. Navigation Meshes for Realistic Multi-Layered Environments. In IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS'11), pp. 3526-3532, 2011.

  

  

• Wouter G. van Toll, Atlas F. Cook IV and Roland Geraerts. Multi-Layered Navigation Meshes. In ASCI - IPA - SIKS tracks, ICT.OPEN (ICT.OPEN 2011), pp. 317-323, 2011.
  This paper has received the best paper award ASCI 2011.

  

  

Software

The software for generating layered navigation meshes is described here.

Movie

The method is demonstrated in the following movie.

Input

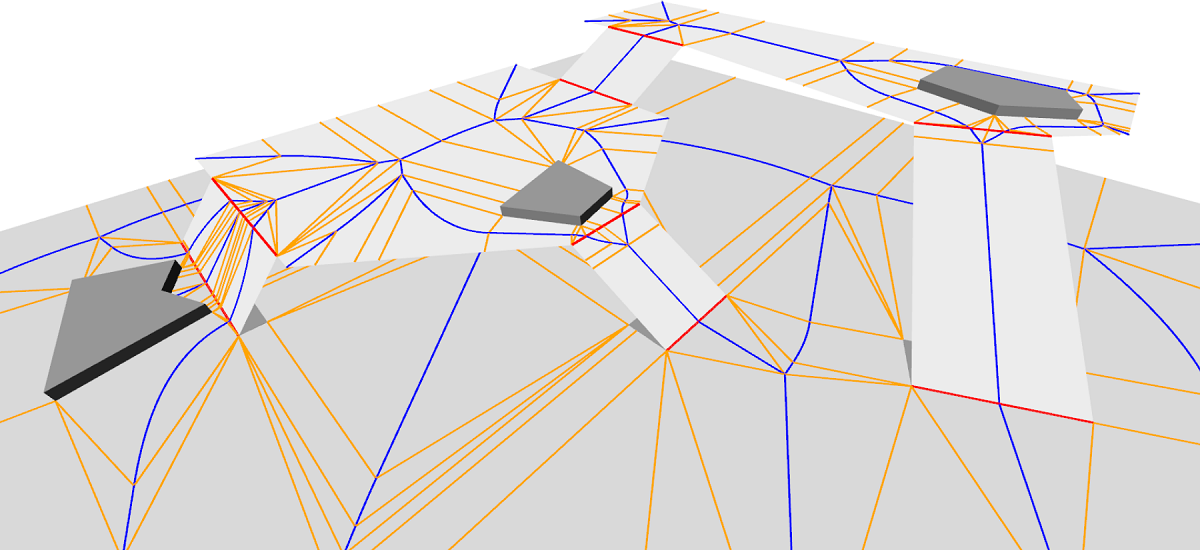
The input for our algorithm is a multi-layered environment.

A simple 3D environment for which we want to compute a navigation mesh.

The initial input is a 3D environment, which consists of a collection of polygons in 3D. From this environment, a walkable environment (WE) is extracted, which is a set of polygons along which characters can walk. A multi-layered environment (MLE) is then a subdivision of the WE into 2D layers. Connections between layers are shown as bold line segments in this example. Please refer to our overview on how a multi-layered environment can be extracted from a 3D environment.

Technique

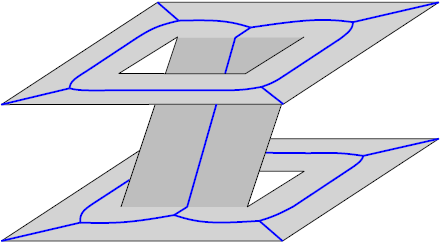
First, a medial axis is computed for each layer using standard techniques. Then, interatively, each connection C_ij is opened. (a). Initially, C_ij is an obstacle on both sides, S_i and S_j. (b). 2D shows a top view of the area around C_ij. The influence zone Z_ij = Z_i + Z_j is shaded. The obstacle points N_ij = N_i + N_j that are nearest to Z_ij are shown in bold black. (c) When opening C_ij, the medial axis changes only inside Z_ij. This medial axis M_Z is defined by N_ij .

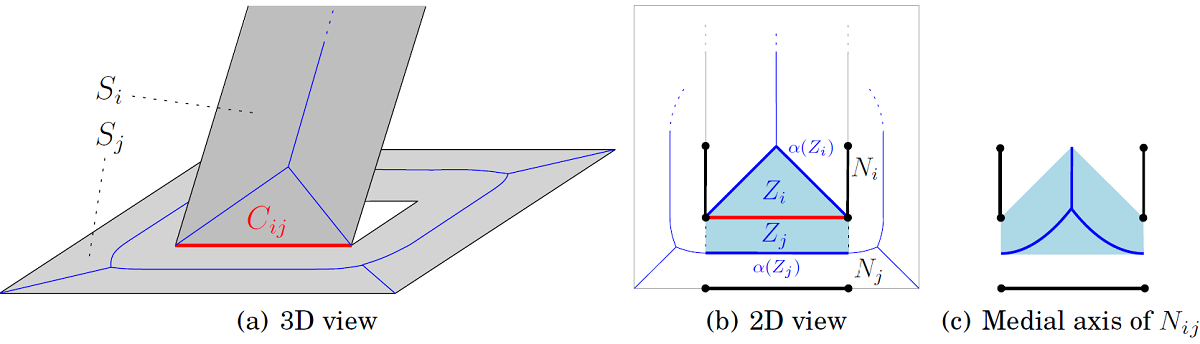
Opening a connection in a multi-layered environment.

We compute the medial axis M_Z in three steps. Figure (a) shows the medial axis when C_ij is still closed. (b) M_Z,i uses only the obstacles of N_i and assumes that Z_j extends to infinity. We compute it using a plane sweep on the ground plane P, starting with the sweep line L at C_ij, without explicitly projecting all of N_i onto P at the same time. (c) Analogously, M_Z,j uses only N_j. (d) We merge the two parts to obtain M_Z.

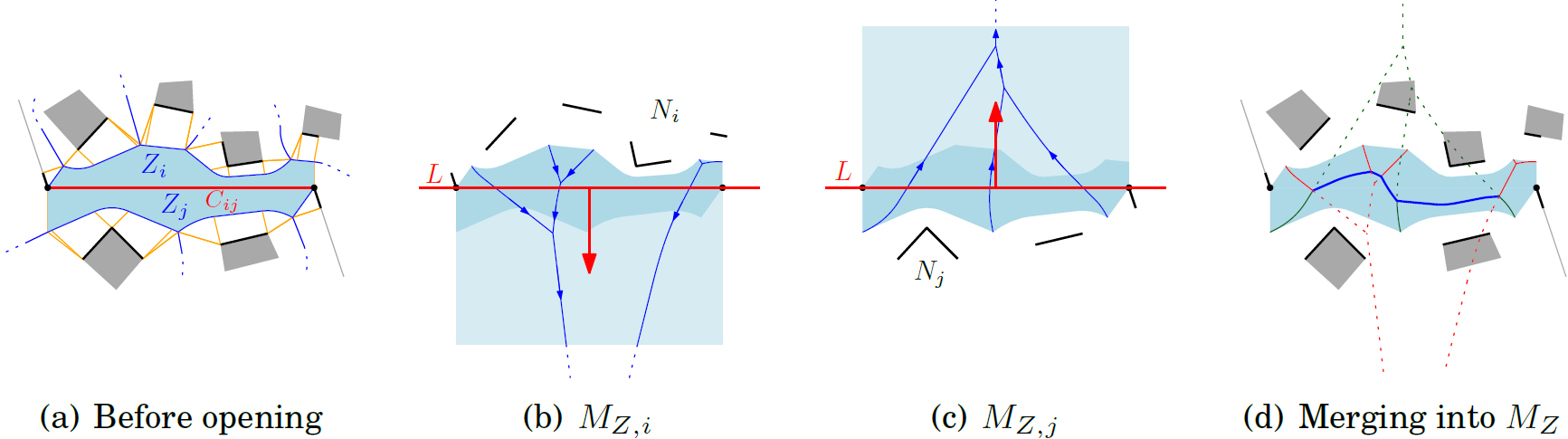
Computation of the medial axis (in a multi-layared environment) in three steps.

Application: The Explicit Corridor Map

The Explicit Corridor Map (ECM) is a navigation mesh that is closely related to the medial axis. Figure (a) shows the medial axis of a 2D environment. The ECM in (b) is a medial axis with nearest-obstacle annotations, shown as orange line segments between vertices and their nearest obstacle points. These segments are not edges in the graph. In figure (c), you can find details of an ECM edge with four bending points. Each bending point bp_k stores its position p_k and its nearest obstacle points l_k and r_k.

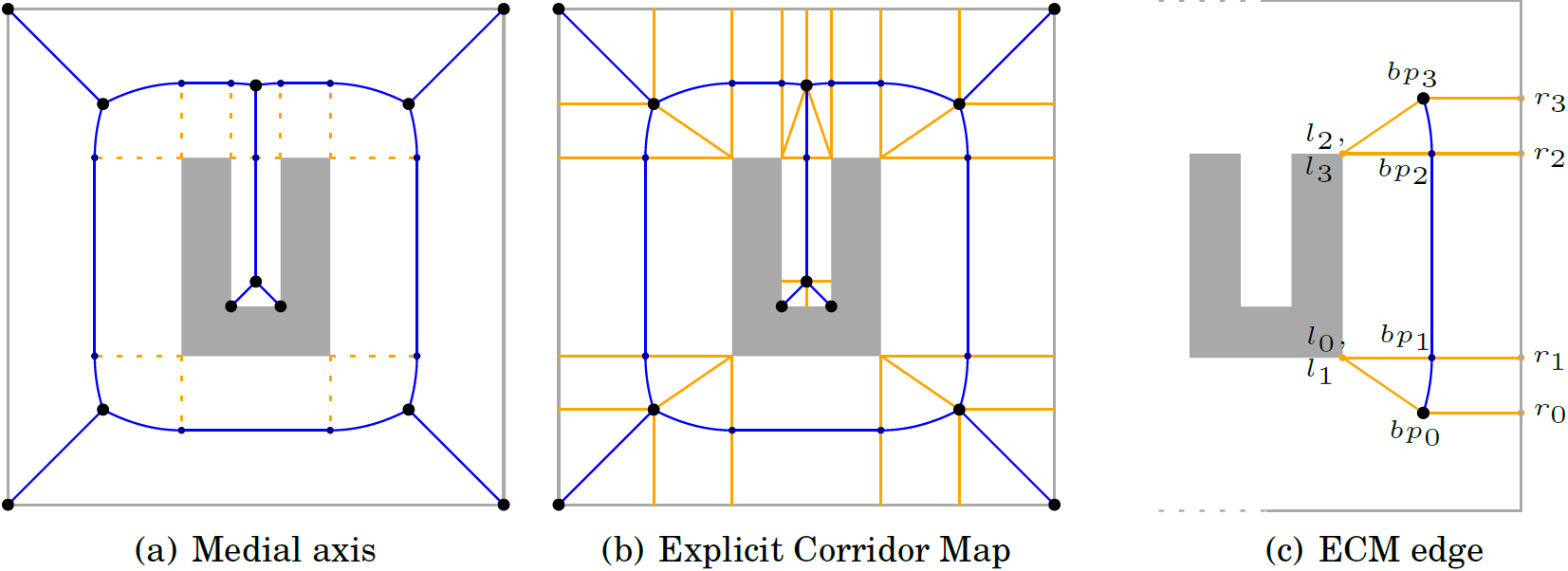
The Explicit Corridor Map is easily derived from a medial axis.

Figure (a) shows some examples of query points (shown as large dots), their nearest obstacle points (small dots), and their retractions (circles). Given two positions s and g in figure (b), the retraction method is used to compute a path from s to g along the medial axis. A corridor describes the free space around this path. (c) Within the corridor, we can compute various types of indicative routes, e.g. with an amount of preferred clearance.

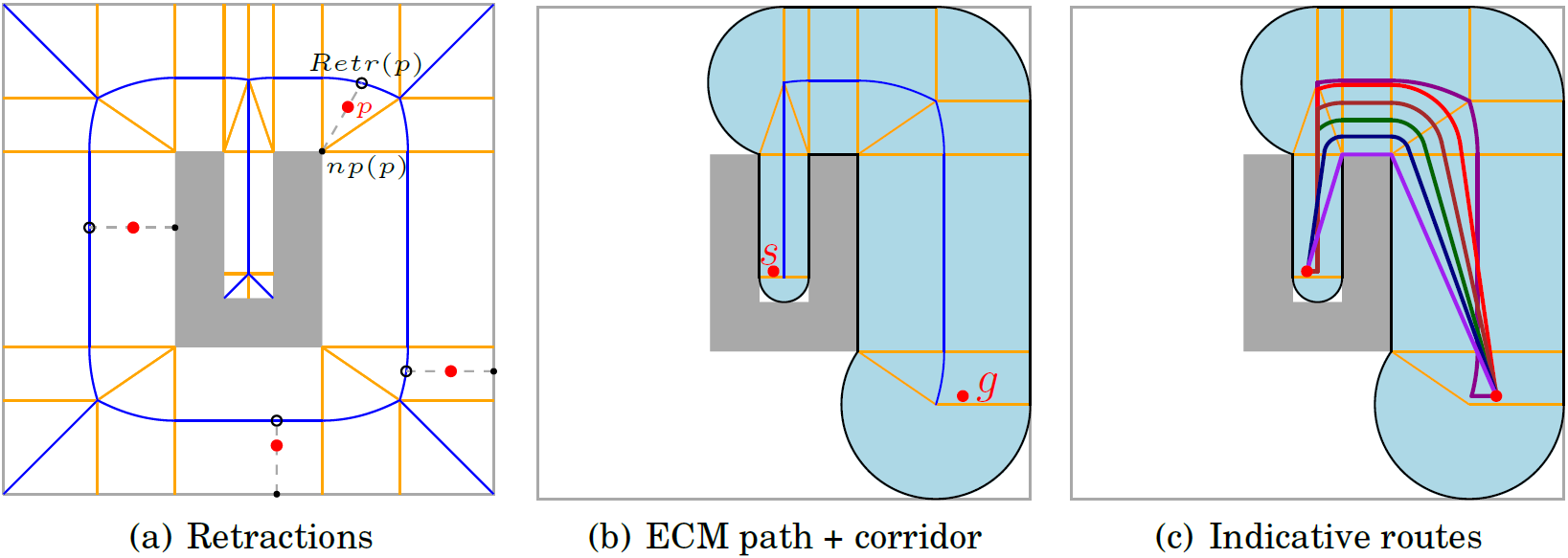
Some key operations defined on the Explicit Corridor Map..

Experiments

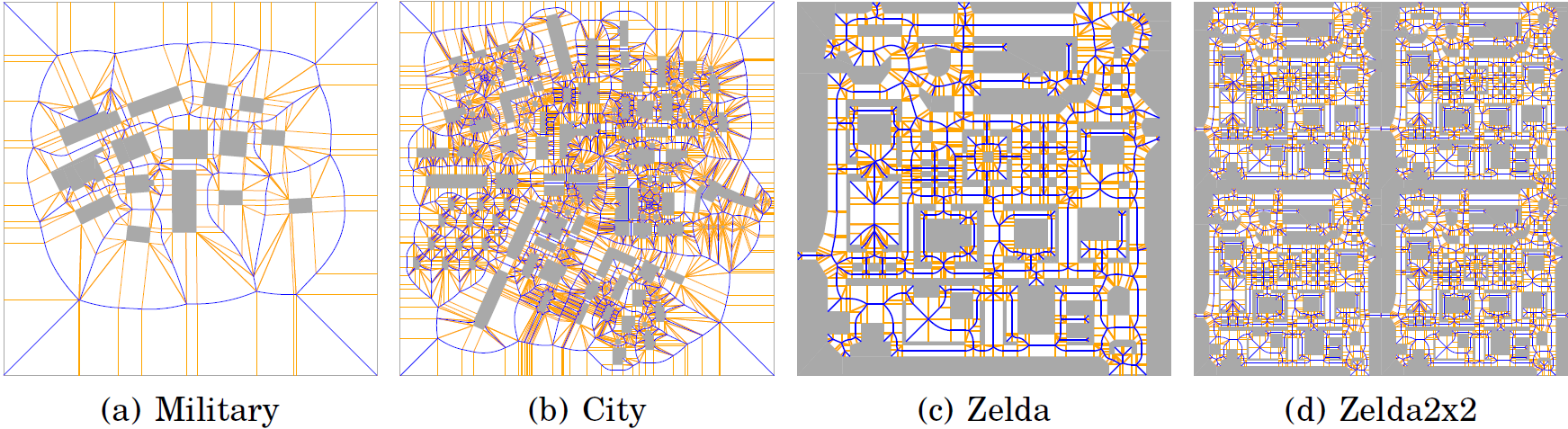
The set of 2D environments and their ECMs.

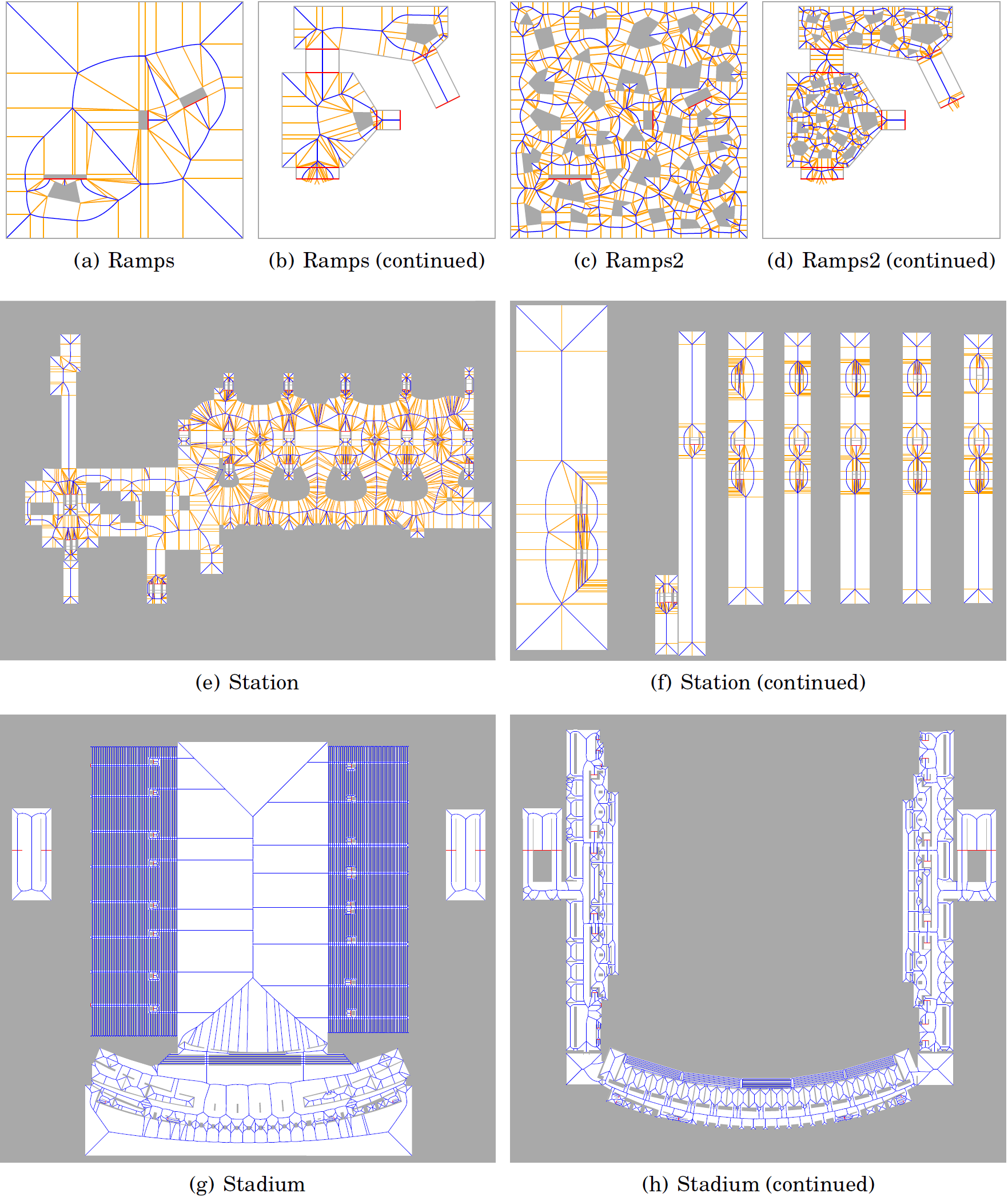
The set of 3D environments and their ECMs (part 1).

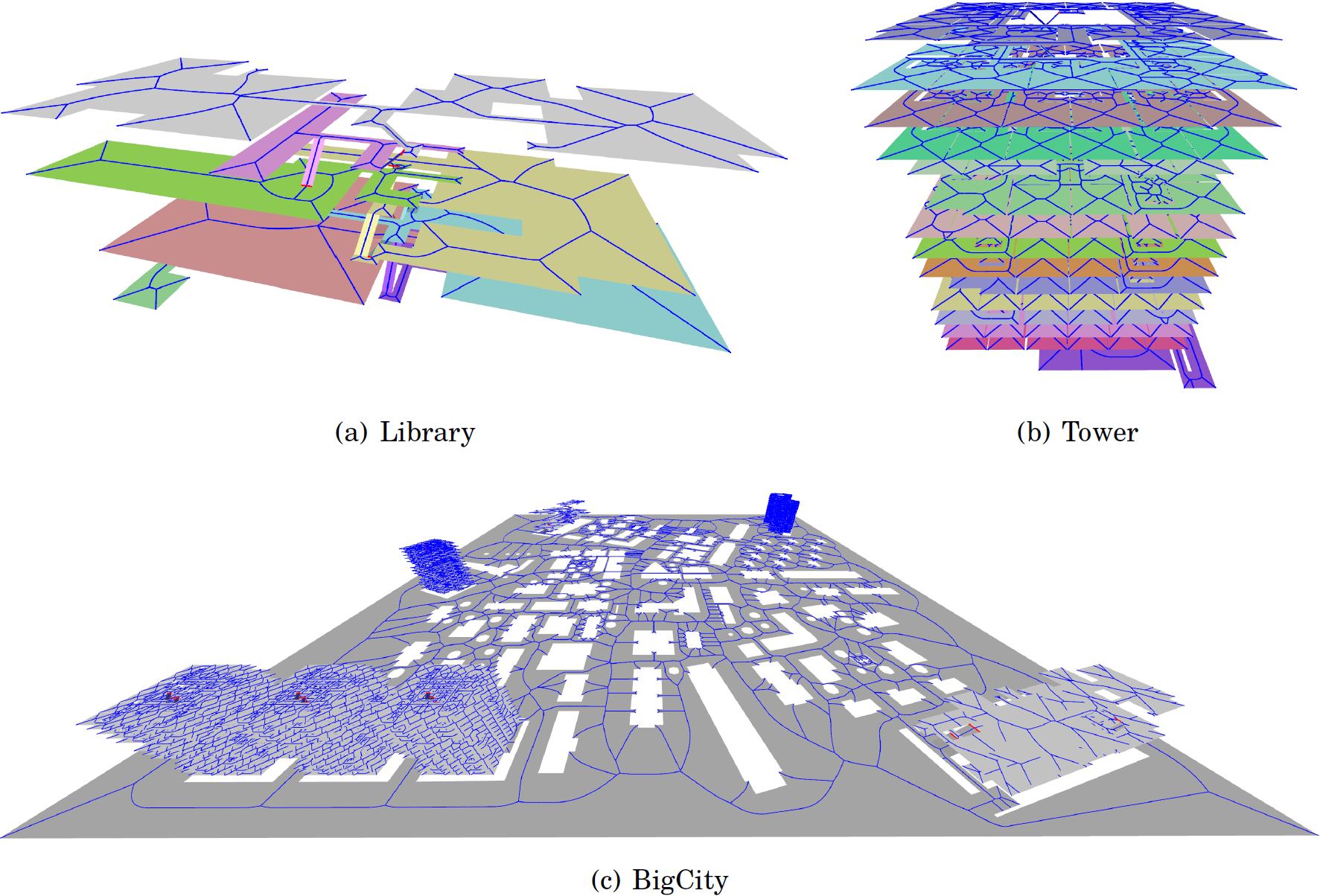
The set of 3D environments and their ECMs (part 2).

Such a mesh also allows dynamic updates when an obstacle is inserted, deleted or moved.

Results

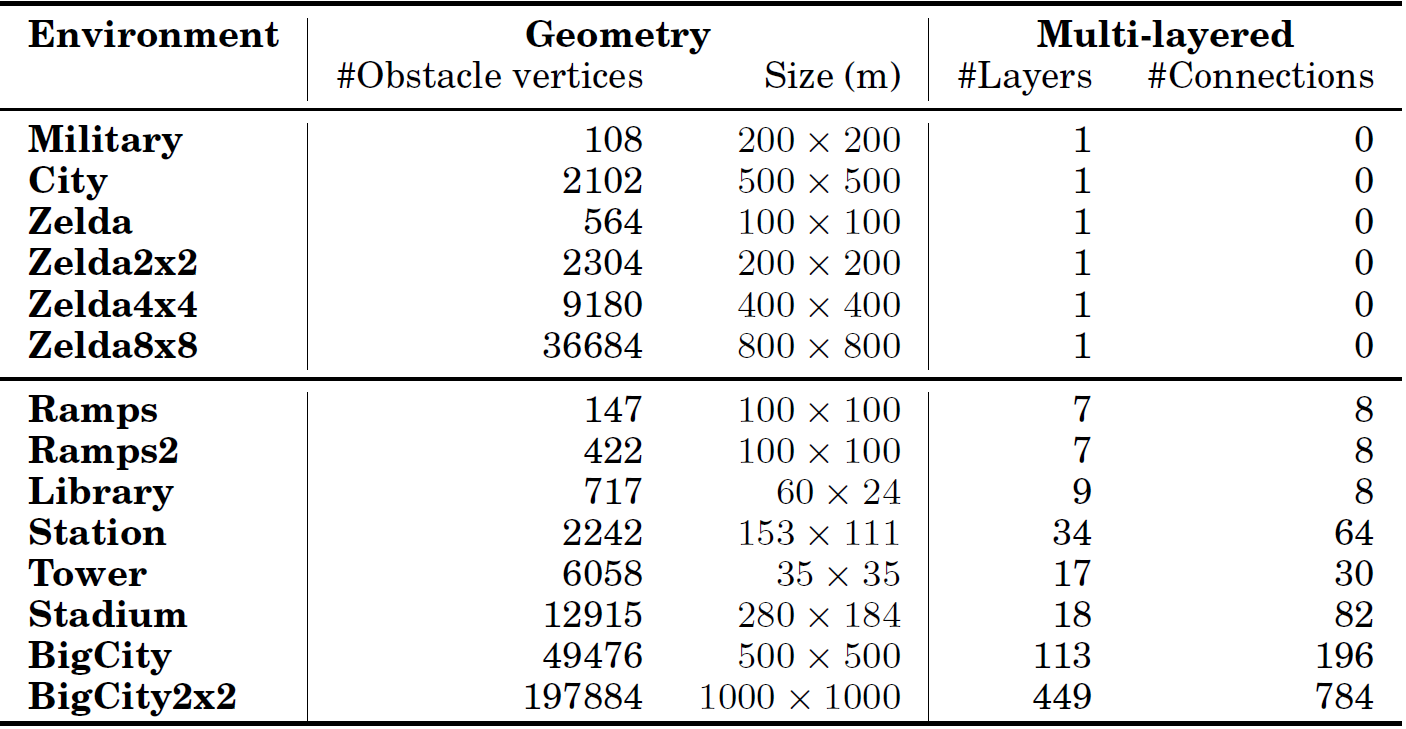
Details of the environments used in our experiments.

Here are the results for all tested environment. The ECM complexity columns show the number of vertices, edges, and bending points in the ECM computed using Boost. The ECM time columns show the ECM construction time for the three implementations: Vroni, Boost, and Boost with 5 parallel threads (for multi-layered environments). All times are in milliseconds and have been averaged over 10 runs. Standard deviations are shown between square brackets.

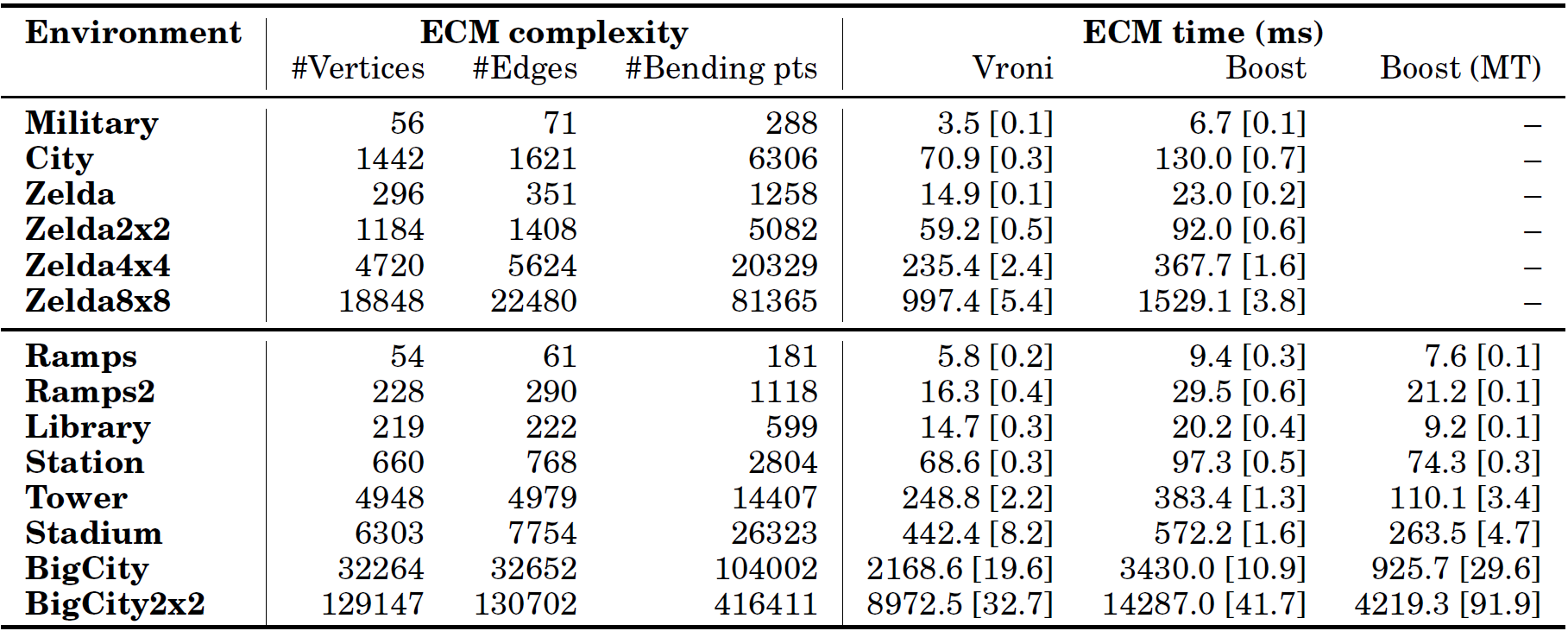
Details of the ECMs for our experiments.

Conclusions

In robotics, simulations, and gaming applications, virtual walking characters often need to compute and traverse paths through an environment. A navigation mesh is a subdivision of the free space into polygons that allows real-time path planning for crowds of characters.

With this application area in mind, we have studied the medial axis for 3D environments with a consistent direction of gravity. A walkable environment (WE) describes where characters can walk. A multi-layered environment (MLE) is a WE that has been subdivided into 2D layers connected by k connections with certain geometric properties. We have defined the medial axis for WEs and MLEs based on projected distances on the ground plane. We have presented an algorithm that computes this medial axis by initially treating all connections as closed obstacles and then opening them incrementally. Compared to previous work [van Toll et al. 2011], we have presented a new and correct algorithm for opening a connection, and we have improved the overall running time to O(n log n log k) by opening the connections in an efficient order.

We have presented an improved definition of the Explicit Corridor Map (ECM), which is a navigation mesh based on the medial axis. The ECM enables path planning for disk-shaped characters of any radius. It supports efficient geometric operations such as retractions, nearest-obstacle queries, dynamic updates, and the computation of short paths with preferred clearance to obstacles.

Our implementation computes the ECM efficiently for large 2D and multi-layered environments. The ECM supports important applications and operations, such as path planning and dynamic updates. It is a useful basis for simulating large crowds of heterogeneous characters in real-time.