Abstract
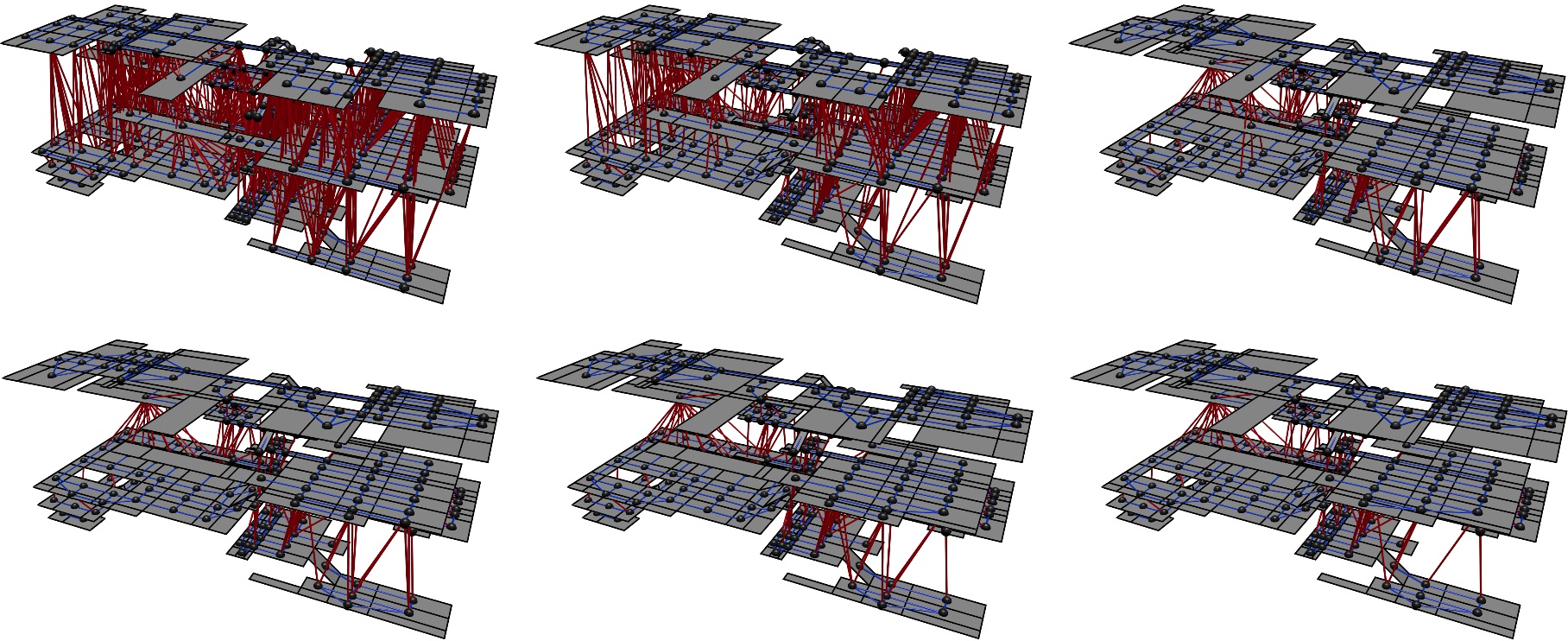
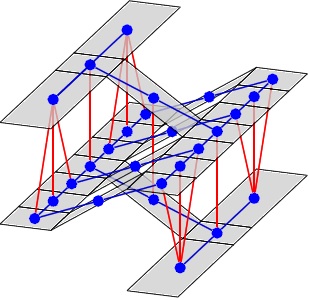
A multi-layered environment is a representation of the walkable space in a 3D virtual environment that comprises a set of two-dimensional layers together with the locations where the different layers touch, which are called connections. This representation can be used for crowd simulations, e.g. to determine evacuation times in complex buildings. Since the execution times of many algorithms depend on the number of connections, we will study multi-layered environments with a minimal number of connections. We show how finding a minimally connected multi-layered environment can be formulated as an instance of the multicut problem. We will prove that finding a minimally connected multi-layered environment is an NP-Hard problem. Lastly, we will present techniques which shrink the size of the underlying graph by removing redundant information. These techniques decrease the input size for algorithms that use this representation for finding multi-layered environments.
Reference
-
Arne Hillebrand, Marjan van den Akker, Roland Geraerts and Han Hoogeveen. Performing Multicut on Walkable Environments: Obtaining a Minimally Connected Multi-Layered Environment from a Walkable Environment. In 10th Annual International Conference on Combinatorial Optimization and Applications (COCOA), LNCS 10043, pp. 311-325, 2016.
Heuristics are proposed and experiments are performed on many environments in our follow-up paper: Separating a Walkable Environment into Layers.