Visualization and Graphics ➤ Interaction ➤ Dept ICS ➤ Faculty of Science ➤ UU

//webspace.science.uu.nl/~telea001/Site/TopBar

Deep Learning Inverse Projections

Projections are the method of choice for mapping high-dimensional data to 2D or 3D scatterplots which can be next easily visualized. In several applications, it is necessary however to do the inverse operation: Given a (2D or 3D) point in the space of such a scatterplot, which high-dimensional point corresponds to it?

Method

We propose a method to compute such inverse projections using deep learning. The technique is very simple to implement, generic (handles any direct projection method), and fast. It works as follows

  • given a direct projection technique, one constructs several 2D projections of one or more datasets
  • we train a neural network to learn the mapping from high dimensions to 2D from the above data
  • we then use the network to infer the high-dimensional position of any 2D point

Applications

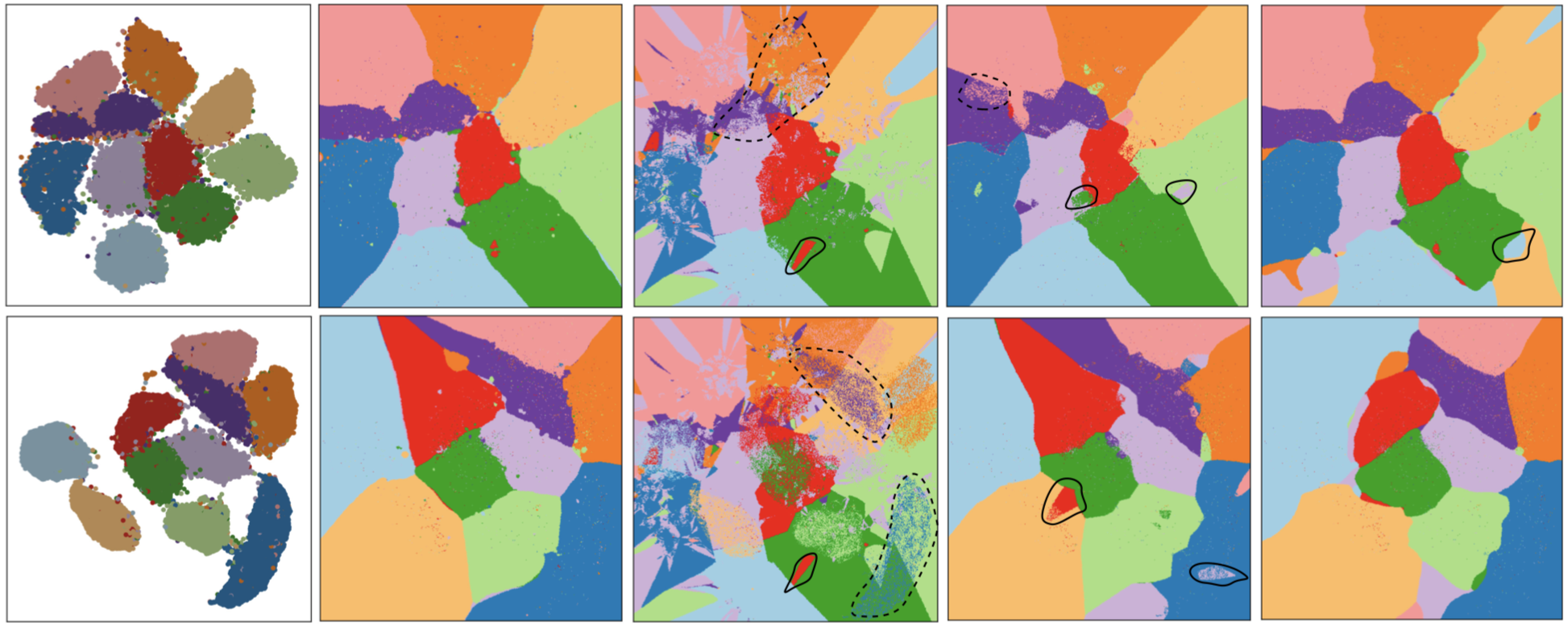
The image below shows how inverse projections can be used. Given a 2D projection of a labeled dataset (left column), we can construct a dense map showing the high-dimensional sample label that corresponds to every 2D pixel. This effectively partitions the 2D image space into decision zones corresponding to a classifier trained on the labeled data. Columns 2-5 show such dense maps constructed by iLAMP, RBF (clusters), RBF (fixed control points), and our method. Our method constructs cleaner decision zones and runs much faster than RBF and iLAMP.

References

Deep Learning Inverse Multidimensional Projections M. Espadoto, F. C. M. Rodrigues, N. S. T. Hirata, R. Hirata Jr, A. Telea. Proc. EuroVA, 2019

UnProjection: Leveraging Inverse-Projections for Visual Analytics of High-Dimensional Data M. Espadoto, G. Appleby, A. Suh, D. Cashman, M. Li, C. Scheidegger, E. Anderson, R. Chang, A. Telea. IEEE TVCG, 2021

Self-Supervised Dimensionality Reduction with Neural Networks and Pseudo-labeling M. Espadoto, N. Hirata, A. Telea. Proc. IVAPP

Improving Self-Supervised Dimensionality Reduction: Exploring Hyperparameters and Pseudo-labeling Strategies A. Oliveira, M. Espadoto, R. Hirata, N. Hirata, A. Telea. Springer CCIS 1691, 135-161