Principal Graph Computation by Skeletons

Principal curves (PCs) are a well-known unidimensional descriptor of scatterplots. Principal graphs (PGs) generalize PCs for scatterplots having a complex topology. Intuitively, PGs are sets of curves locally centered in the density distribution of scatterplot points. Constructing PCs and PGs is, however, complex and slow with existing methods.

Method

We solve the above problems by using 2D skeletons. Given a 2D scatterplot, we reduce it to a continuous density field by kernel density estimation, and compute a binary shape by thresholding this field. Next, we compute a 2D skeleton of this shape using the fast, accurate, and noise-resistant AFMM method. Finally, we iteratively shift this skeleton to match the local density center. The entire process is simple to implement and executes in a few seconds on a modern PC.

Results

The image below shows PGs for several scatterplots computed from ground-truth generating curves (left column). The next columns show PGs computed by the KPG method, the SCMS method, and our method (SPG). Our method is of at least the same quality as KPG and SCMS with respect to approximating the ground truth.

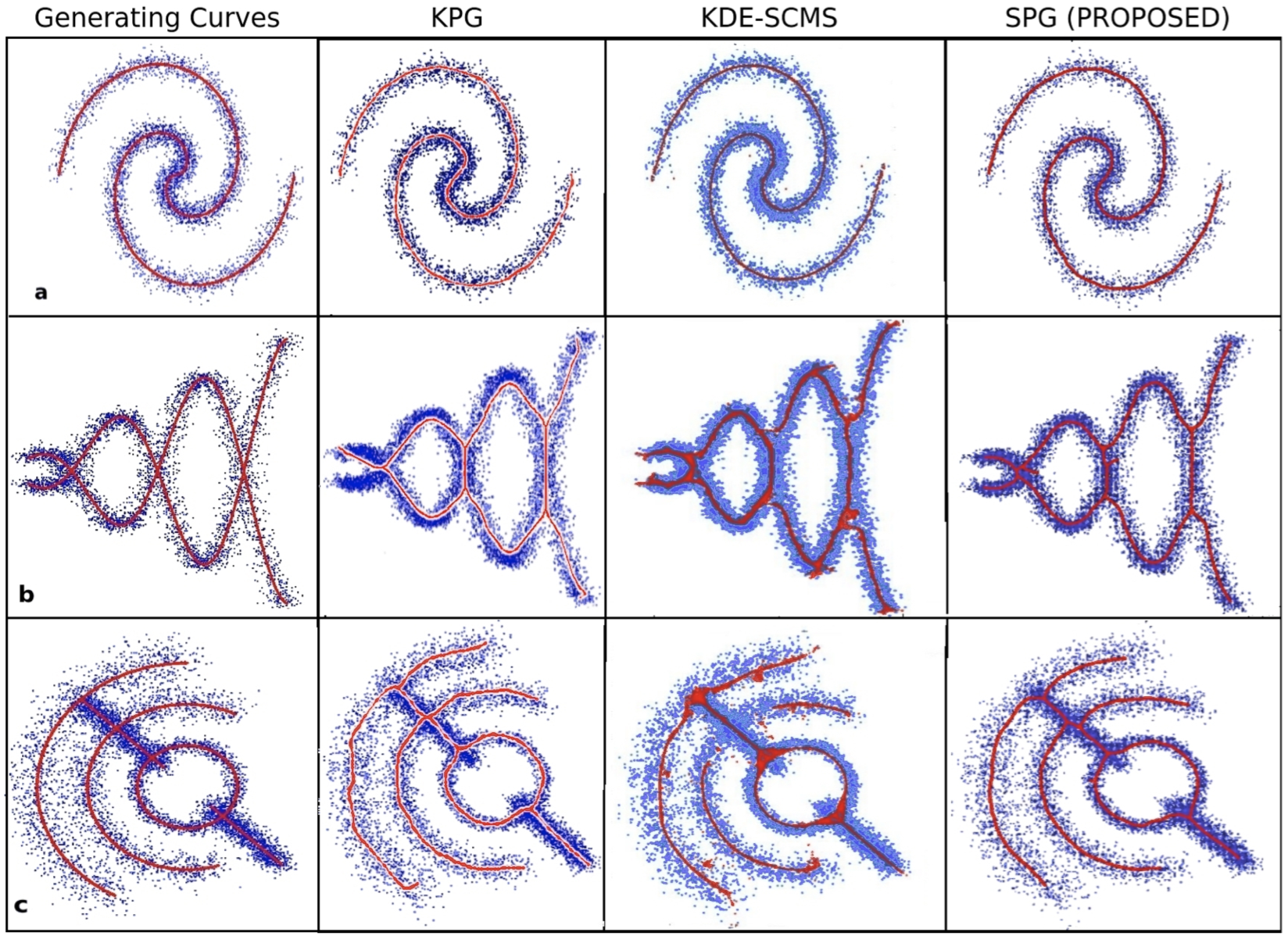
Image based technique

Our PG construction works fully image based, that is, using 2D image processing operations. This makes it easily parallelizable, computationally efficient, and simple to implement. We also used image-based techniques for bundle drawing, skeleton based bundling, kernel density graph bundling, and CUDA graph bundling.

Publications

Scatterplot Summarization by Constructing Fast and Robust Principal Graphs from Skeletons J. Matute, M. Fischer, A. Telea, L. Linsen. Proc. IEEE PacificVis 2019

Skeleton-based Scagnostics J. A. Matute Flores, L. Linsen, A. Telea. IEEE TVCG 24(1), pp. 542-552, 2018