Interactive 3D Shape Rotation Using 2D Skeletons
Rotating 3D shapes is difficult. Imagine a typical 3D viewer in which you have a complex 3D shape. How to ``specify`` the rotation of this shape ``easily''?
Typical mechanisms include virtual trackball, which is easy to use but hard to control, or axis-aligned rotation, which is easy to use and control, but limited in flexibility.
Shape-based rotation
We propose to support users in rotating shapes along their natural symmetry axes. In detail
- local symmetry axes are computed from a 2D projection (view) of any 3D shape, using image skeletons
- these 2D axes are back-projected to 3D using a simple approximation
- the shape is rotated along the emerging 3D axes
Pipeline
Our skeleton-based rotation tool is surprisingly simple to implement. The pipeline is below:
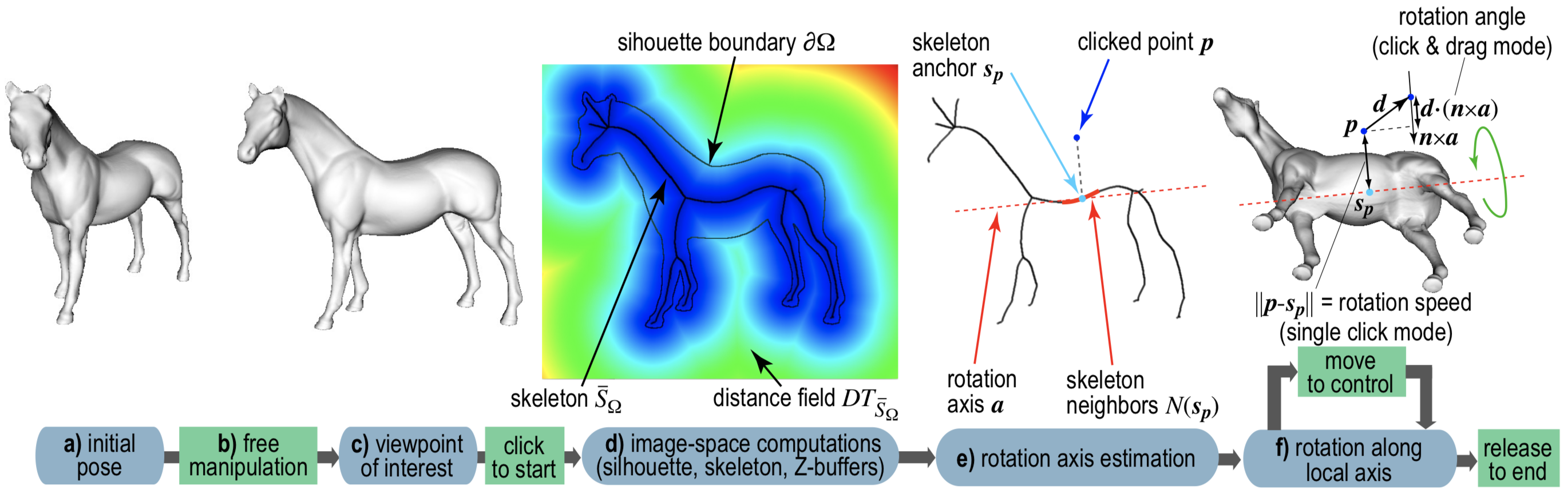
- select any viewpoint, e.g. using trackball (a-c)
- compute the silhouette of the 3D shape in that view (d)
- compute the 2D skeleton of the silhouette (d)
- fit a 2D line to skeleton points close to the mouse pointer (e)
- backproject the 2D line to 3D (e)
- rotate the shape around the 3D line based on mouse motion (f)
Features
This method is surprisingly simple, fast, and generic, since
- 2D image skeletons can be computed in real-time (see CUDASkel)
- it works for anything whose 2D silhouette can be computed (polygon meshes, polygon soups, splats)
- it only requires a click and drag in the window (so, suitable also for touch interfaces)
- all computations can be done very efficiently on the GPU (NVidia CUDA)
- it integrates with any 3D renderer
Videos
A video illustrating the interactive 3D axis rotation is available below
Implementation
The method is implemented in C++ using OpenGL1.1 and NVidia CUDA. Sample code is available here.
Publications
Interactive Axis-Based 3D Rotation Specification Using Image Skeletons X. Zhai, X. Chen, L. Yu, A. Telea. Proc. GRAPP, 2020
