Multiscale 3D Skeletonization of Polygonal Models
Skeletonization of 3D shapes is a challenging area of research. Practical applications thereof pose a complex set of requirements, including correctness, completeness, robustness to noise, handling any 3D shape, and computational (memory and speed) efficiency. These requirements, as well as the fundamentals of skeletonization, are described separately in an associated project here.
Polygonal models
3D models come in two main flavors: voxel volumes and polygonal models, or meshes. Meshes have several important advantages: compact surface representation, easy modeling of non-uniform surface detail, and a vast repository of processing tools and available models.
However, computing surface skeletons of complex 3D meshes was still a challenging task. Until now.
3D Mesh Skeletonization Algorithm
We developed a skeletonization algorithm for 3D meshes which
- can handle very complex shapes such as produced by the 3D modeling industry
- computes arbitrarily exact, compact, 3D "surface" skeletons (manifolds)
- produces the skeleton both as a point cloud and a triangle mesh
- deals with noisy shapes using a multiscale importance metric
- accurately reconstructs the initial shape in real-time from its skeleton
- is to our knowledge the world's fastest 3D-mesh surface-skeletonization method
- runs on commodity graphics PCs with limited memory resources
- is inherently parallelizable
- requires no user parameters
Step 1: Skeleton point cloud extraction
First, we extract the skeleton from a given 3D mesh. For this, we use a fast 'ball shrinking' method which reduces balls tangent to each mesh vertex until they contain exactly two points. The centers of such balls are located on the skeleton.
Careful algorithm design, using a bisection-like method, , and parallelization, allow us to deliver high speed. For example, the models below, containing hundreds of thousands of triangles, are skeletonized in sub-minute time on a dual-core MacBook Pro laptop running at 2.5 GHz.




The skeleton points are colored by the well-known feature-vector cosine angle metric (blue points correspond to parallel shape areas, red points to shape convexities).
Step 2: Multiscale importance
For each skeleton point, we compute an "importance metric" which describes the amount of area encoded by that point. For this, we adapt the geodesic-based method described in this paper to polygonal meshes. We compute all geodesics directly using CUDA, which delivers almost two orders of magnitude speed-up as compared to a sequential CPU implementation.
The importance metric is shown below. Red points encode large object areas, such as the rump. Blue points encode small features, such as edges or leg tips.
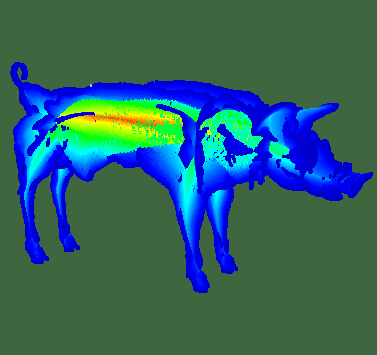
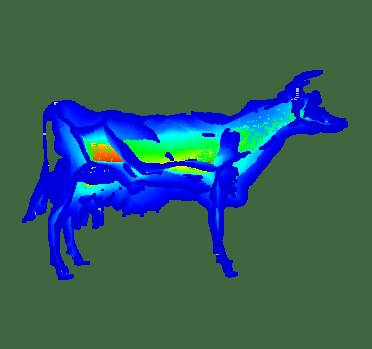
Thresholding this metric delivers a multiscale of nested skeletons.
Step 3: Splatting reconstruction
We reconstruct the shape from the skeleton point cloud by splatting 'shaded balls' (encoded as luminance-depth textures) on screen-aligned billboards centered at the skeleton points. This delivers a near-pixel-accurate shape reconstruction at several frames per second (left image below). In contrast, rendering 3D polygonal balls delivers less accuracy at around 20 times less speed (see the zoomed-in images below)




Here are the reconstructions for the cow model (left: splats; right: 3D geometric balls):




Step 4: Skeleton reconstruction
We reconstruct the 3D skeleton as a set of intersecting manifolds. Two methods are provided here:
- a method using Delaunay triangulation of quasi-flat shape projections on the skeleton
- a method based on an adaption of the ball-pivoting algorithm
The Delaunay method (below left) is fast: 10 seconds for a 300K skeleton point cloud), but delivers more polygons and a less clean mesh. The ball-pivoting method (below right) is slower (40 seconds for the same cloud) but delivers less polygons and a clean mesh.




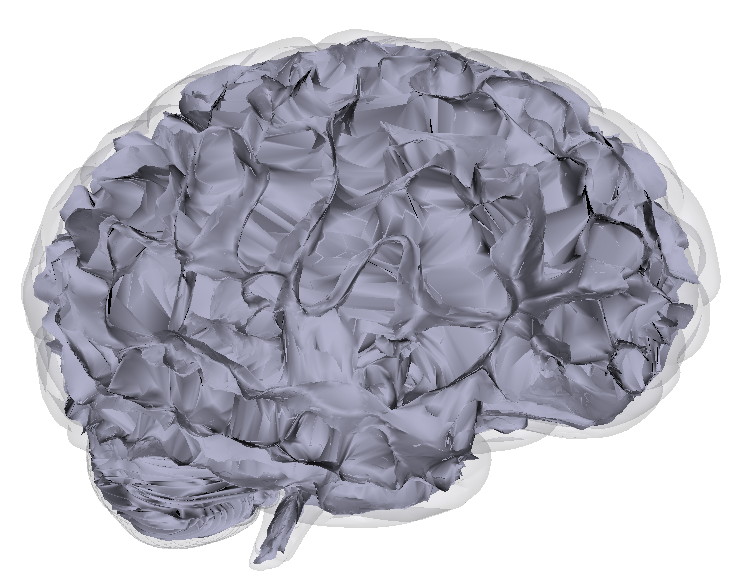
The image below shows the surface skeleton of a brain surface. Note how the skeletal manifolds nicely capture the anatomical shapes (sulci and gyri) on the cortex surface.
Nonphotorealistic rendering
The skeleton structure can be used to create real-time nonphotorealistic shape renderings (NPR). The example below shows the cow model, rendered with splats whose shape is a prism rather than a sphere. Next, we enhance the contrast of the image to obtain a 'stylized' rendering appearance.

The examples below show a different NPR technique. Here, we
- select all skeleton points with a lower importance
- select all shape points corresponding to the above skeleton points
- for each such point, set its normal to the normal of the closest surface point corresponding to an important skeleton point




This creates a 'faceted' look. Points close to the (implicitly detected) shape edges get their normals from flat neighborhoods. This accentuates the transitions between such flat neighborhoods. Note that the shape is not changed, just its normals.
Comparison
Compared with its closest-resembling skeletonization technique (based on voxels), our method is roughly ten times faster, takes ten times less memory, and captures significantly more detail due to the non-uniform point placement. Practically, you can obtain a surface skeleton of a 3D mesh shape of 1 million points in under a second on a 2014 consumer-grade PC with an NVidia card
Acknowledgements
This method has been developed in collaboration with dr. Andrei Jalba (Univ. of Eindhoven) and Jacek Kustra (Philips Research). Thanks go also to Madalina Florean (Univ. Transilvania, Brasov, Romania) for her MSc work on this topic. This work was partially supported by the grant PN-II-RU-TE-2011-3-2049 Image-assisted diagnosis and prognosis of cutaneous melanocitary tumors offered by ANCS, Romania.
Availability
Coming soon; please contact me (Alex Telea) if you are really interested in this.
Publications
1. A. Jalba, A. Kustra, A. Telea (2013) Surface and Curve Skeletonization of Large 3D Models on the GPU, IEEE TPAMI 35(6), pp. 1495-1508 (PDF)
