Unified Multiscale Planar, Surface, and Curve Skeletons

Question

Skeletons, or medial axes, are structures that researchers have aimed to compute for more than half a century to concisely describe 2D and 3D shapes. There are two key problems for their computation:

• regularization: How to eliminate the effects of small-scale noise on the shape to get clean, useful, skeletons;
• generalization: How to compute regularized skeletons of 2D and 3D shapes using the same principle.

Solution

We have found the solution to both above problems (after elusive searches in the same direction for decades and by tens of researchers). Simply put: We model skeletonization as an advection process that moves mass, uniformly spread on a shape's boundary, inwards, following a momentum-conservation principle:

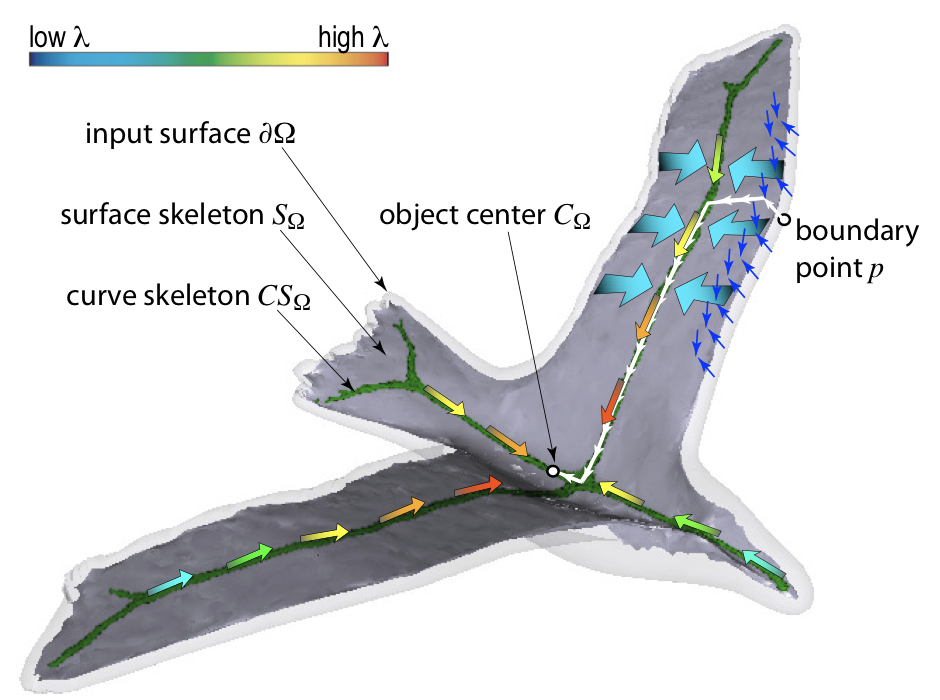
Mass flows from the shape boundary inwards along the gradient of the boundary's distance transform. When different mass particles collide (that is, on the surface skeleton), they move in the direction that obeys momentum conservation. Such mass particles collide again along the curve skeleton. Ultimately, all mass sinks in a single point, the shape's center. Skeletonization, using a single principle and model, regardless of dimensionality!

Results

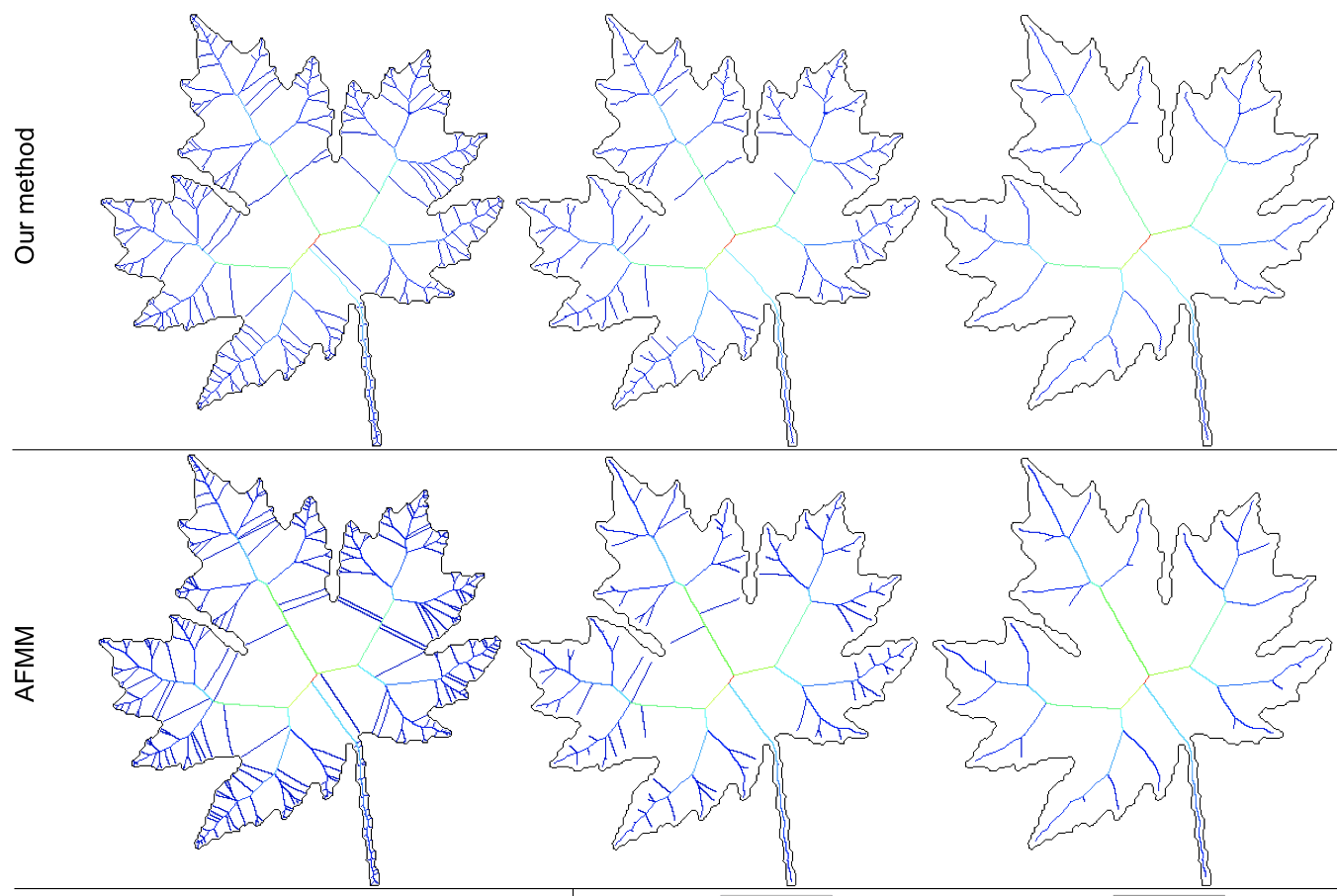
Our method gives visually identical results to more complex, dimension-specific, skeletonization methods. See below an example in 2D:

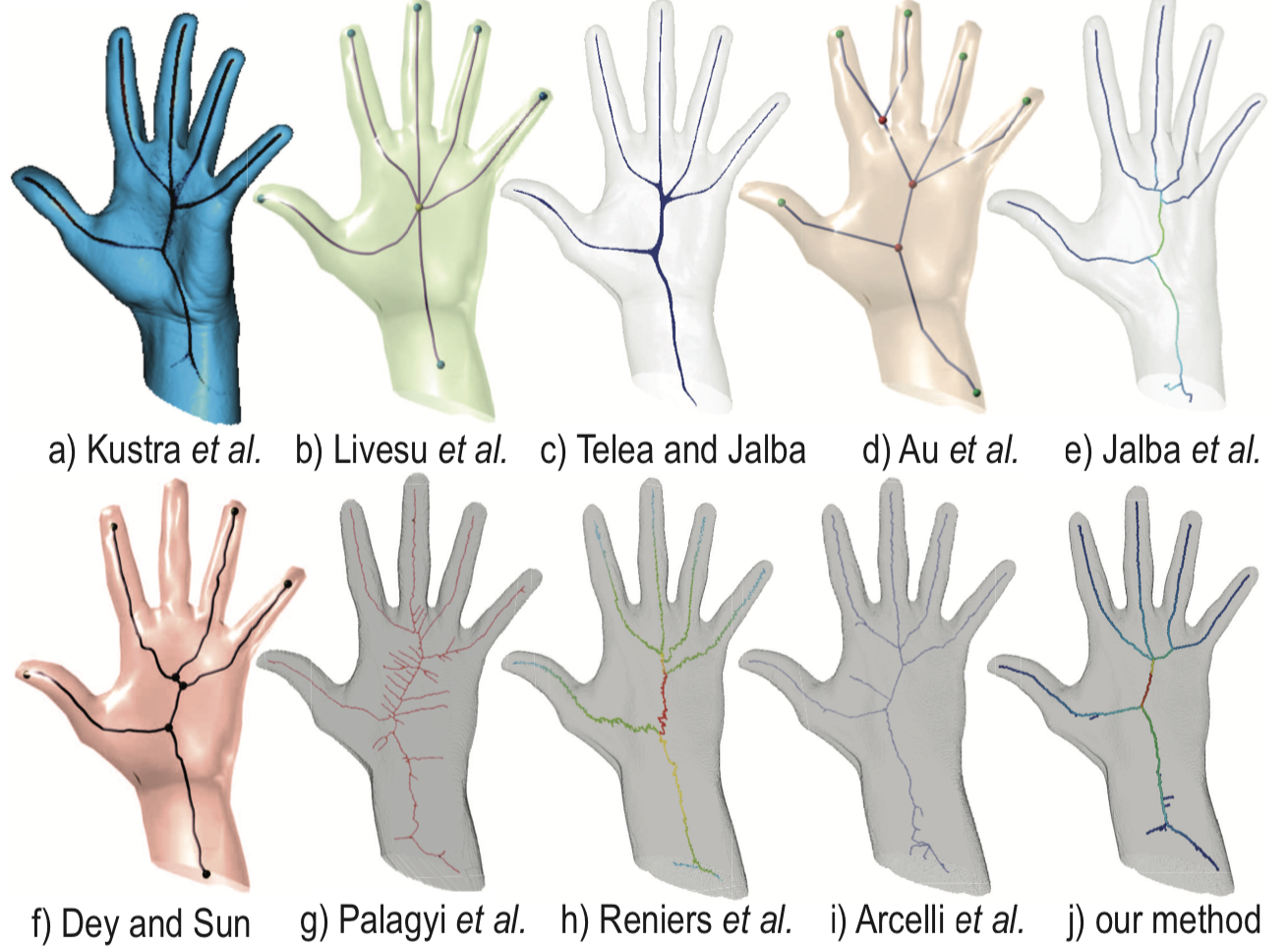
Even more impressively, we get the same visually identical results for our method compared to 3D skeletonization techniques:

Publications

An Unified Multiscale Framework for Planar, Surface, and Curve Skeletonization A. Jalba, A. Sobiecki, A. Telea. IEEE TPAMI, vol. 38, no. 1, pp. 38-45, 2015